- 是我对课程笔记的梳理和理解,会包含大量的原文内容,英语基础好的建议先自行阅读课程笔记 PDF,然后再阅读我的笔记。
- 同时,推荐在学习的过程中完成对应的作业。
0 数学基础#
A.1 随机向量(Random Vectors,RVs)#
考虑 $d$ 维欧几里得空间中的数据 $x=(x^1,\ldots,x^d)\in\mathbb{R}^d$,其内积为 $\langle x,y\rangle=\sum_{i=1}^d x^i y^i$,相应的范数为 $\|x\|=\sqrt{\langle x,x\rangle}$。
我们将考虑取值于 $\mathbb{R}^d$ 的随机变量(random variables,RVs)$X$,其具有连续型概率密度函数(probability density function,PDF),定义为连续函数
$$ p_X:\mathbb{R}^d\to\mathbb{R}_{\ge 0}, $$并使得事件 $A$ 的概率为
$$ \mathbb{P}(X\in A)=\int_A p_X(x)\,dx. \quad (80) $$其中 $\int p_X(x)\,dx=1$。按约定,当对整个空间积分时,我们省略积分区间(即将 $\int$ 视为 $\int_{\mathbb{R}^d}$)。为简洁起见,我们把随机变量 $X_t$ 的概率密度 $p_{X_t}$ 简记为 $p_t$。我们使用记号 $X\sim p$(或 $X\sim p_X$)表示 $X$ 服从密度 $p$。在生成式建模中,一个常见的 PDF 是 $d$ 维各向同性高斯分布:
$$ \mathcal{N}(x;\mu,\sigma^2 I)=(2\pi\sigma^2)^{-d/2}\exp\!\left(-\frac{\|x-\mu\|_2^2}{2\sigma^2}\right), \quad (81) $$其中 $\mu\in\mathbb{R}^d$、$\sigma\in\mathbb{R}_{>0}$ 分别表示分布的均值与标准差。
随机变量的期望是在最小二乘意义下最接近 $X$ 的常向量:
$$ \mathbb{E}[X] = \mathop{\mathrm{arg\,min}}_{z\in\mathbb{R}^d} \int \lVert x - z \rVert^2 p_X(x)\,\mathrm{d}x = \int x\, p_X(x)\,\mathrm{d}x. \quad (82) $$计算随机变量函数期望的一个有用工具是无意识统计学家法则(law of the unconscious statistician,常简称为 LOTUS):
$$ \mathbb{E}[f(X)]=\int f(x)\,p_X(x)\,dx. \quad (83) $$必要时,我们将用 $\mathbb{E}_X f(X)$ 来显式标明期望所对应的随机变量。
A.2 条件密度与期望(Conditional Densities and Expectations)#
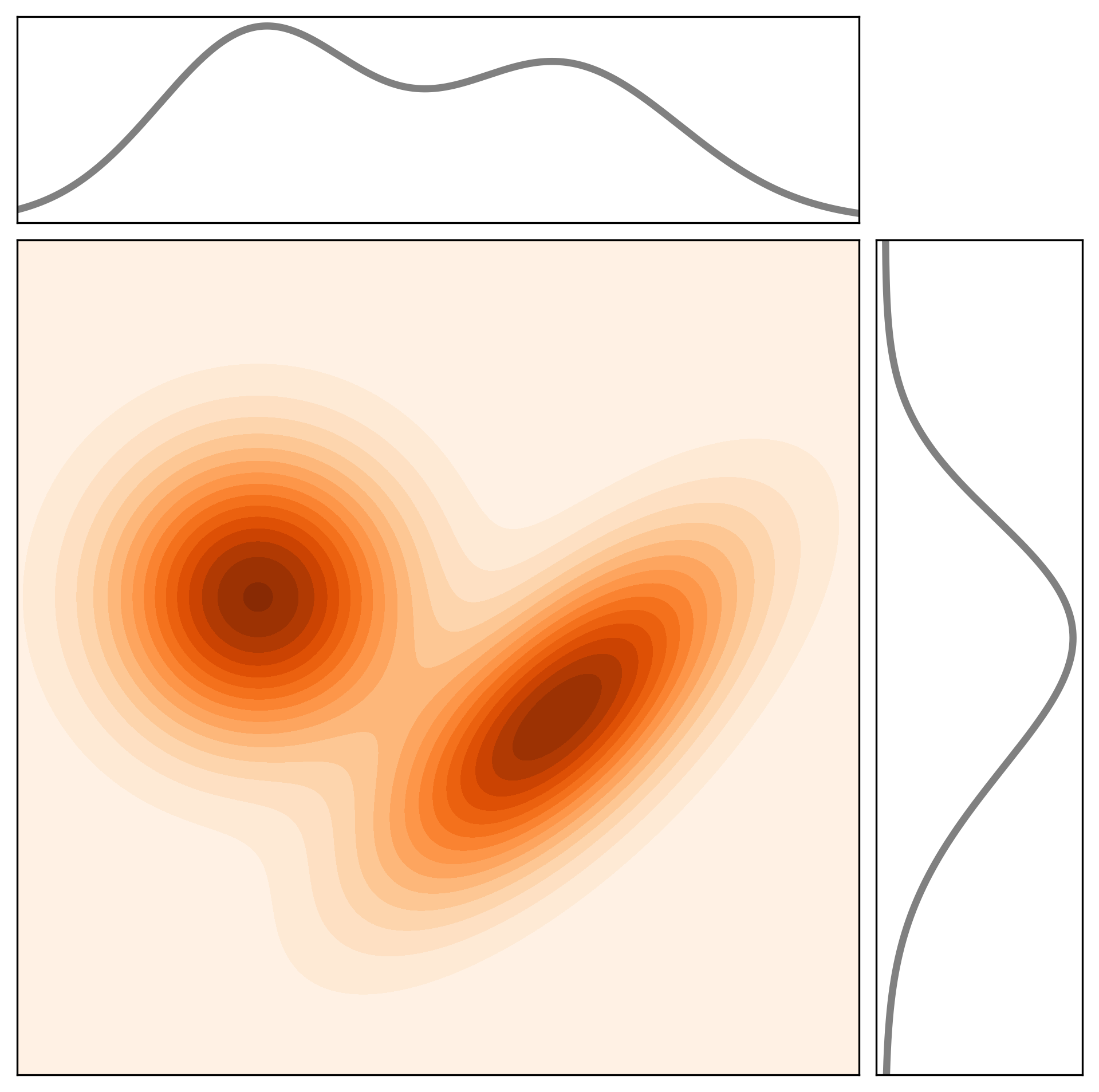
图 16:联合概率密度函数 $p_{X,Y}$(阴影区域)及其边缘分布(亦称边际分布)$p_X$ 和 $p_Y$(黑色曲线)。
给定两个随机变量 $X,Y\in\mathbb{R}^d$,其联合概率密度函数(PDF)$p_{X,Y}(x,y)$ 的边缘密度满足
$$ \int p_{X,Y}(x,y)\,dy \;=\; p_X(x),\qquad \int p_{X,Y}(x,y)\,dx \;=\; p_Y(y). \quad (84) $$参见图 16($d=1$)以获得两个随机变量联合 PDF 的示意图。条件 PDF $p_{X\mid Y}$ 描述在事件 $Y=y$(且 $p_Y(y)>0$)条件下随机变量 $X$ 的 PDF:
$$ p_{X\mid Y}(x\mid y)\;:=\;\frac{p_{X,Y}(x,y)}{p_Y(y)},\qquad \Longrightarrow\qquad p_{X,Y}(x,y)\;=\;p_{X\mid Y}(x\mid y)\,p_Y(y). \quad (85) $$同理可得 $p_{Y\mid X}$。贝叶斯法则把 $p_{Y\mid X}$ 用 $p_{X\mid Y}$ 表示为
$$ p_{Y\mid X}(y\mid x)\;=\;\frac{p_{X\mid Y}(x\mid y)\,p_Y(y)}{p_X(x)},\qquad p_X(x)>0. \quad (86) $$条件期望 $\mathbb{E}[X\mid Y]$ 是在最小二乘意义下逼近 $X$ 的最佳函数 $g_\star(Y)$:
$$ \begin{aligned} g_\star &:= \mathop{\mathrm{arg\,min}}_{g:\mathbb{R}^d\to\mathbb{R}^d} \mathbb{E}\!\left[\|X-g(Y)\|^2\right] \\ &= \mathop{\mathrm{arg\,min}}_{g:\mathbb{R}^d\to\mathbb{R}^d} \iint \|x-g(y)\|^2\,p_{X,Y}(x,y)\,\mathrm{d}x\,\mathrm{d}y\\ &= \mathop{\mathrm{arg\,min}}_{g:\mathbb{R}^d\to\mathbb{R}^d} \int\!\Big[\int \|x-g(y)\|^2\,p_{X\mid Y}(x\mid y)\,\mathrm{d}x\Big]\,p_Y(y)\,\mathrm{d}y . \end{aligned} \quad (87) $$当 $y\in\mathbb{R}^d$ 且 $p_Y(y)>0$ 时,条件期望函数因此为
$$ \mathbb{E}[X\mid Y=y]\;:=\;g_\star(y)\;=\;\int x\,p_{X\mid Y}(x\mid y)\,dx, \quad (88) $$其中第二个等号来自于对式 (87) 内层括号(取 $Y=y$)的极小化,做法与式 (82) 相同。把 $g_\star$ 与随机变量 $Y$ 复合得到
$$ \mathbb{E}[X\mid Y]\;:=\;g_\star(Y), \quad (89) $$它是一个取值于 $\mathbb{R}^d$ 的随机变量。容易混淆的是,$\mathbb{E}[X\mid Y=y]$ 与 $\mathbb{E}[X\mid Y]$ 均被称为“条件期望”,但二者并非同一对象:前者是从 $\mathbb{R}^d\!\to\!\mathbb{R}^d$ 的函数,后者则是一个 $\mathbb{R}^d$ 值的随机变量。以下均使用上述记法以避免歧义。
塔式性质(tower property) 有助于化简涉及条件期望的推导:
$$ \mathbb{E}\!\left[\mathbb{E}[X\mid Y]\right]\;=\;\mathbb{E}[X]. \quad (90) $$由于 $\mathbb{E}[X\mid Y]$ 本身是随机变量(即 $Y$ 的函数),外层期望就是对其再取期望。可由上述定义直接验证:
$$ \begin{aligned} \mathbb{E}\!\left[\mathbb{E}[X\mid Y]\right] &= \int\!\Big(\int x\,p_{X\mid Y}(x\mid y)\,dx\Big)\,p_Y(y)\,dy \\ &\overset{(85)}{=} \iint x\,p_{X,Y}(x,y)\,dx\,dy \\ &\overset{(84)}{=} \int x\,p_X(x)\,dx \;=\;\mathbb{E}[X]. \end{aligned} $$最后,考虑两个任意随机变量 $X$ 与 $Y$ 以及它们的某个函数 $f(X,Y)$。利用无意识统计学家法则并结合式 (88),有
$$ \mathbb{E}\!\left[f(X,Y)\mid Y=y\right]\;=\;\int f(x,y)\,p_{X\mid Y}(x\mid y)\,dx. \quad (91) $$1 介绍(Introduction)#
1.1 概览(Overview)#
近几年,我们都见证了人工智能(AI)领域的一场巨大变革:图像生成器(如 Stable Diffusion 3)能够生成写实或艺术风格的图像,视频模型(如 Meta 的 Movie Gen Video)能够生成高度逼真的短片,大语言模型(如 ChatGPT)能够生成近似“人类水平”的文本回应。这场革命的核心,是 AI 系统获得了一种新的能力:生成对象。相较于过去主要用于“预测”的 AI,新一代生成式 AI 更“有创造力”:它们能够基于用户给定的输入“做梦”,生成新的对象。
本课程的目标是介绍两类最广泛使用的生成式 AI 算法:去噪扩散模型(denoising diffusion models)与 流匹配(flow matching)。它们是当前最强图像、音频、视频生成模型的基础组件(例如 Stable Diffusion 3、Movie Gen Video),并且也已成为某些科学应用中的 SOTA 方法(例如蛋白质结构建模中的 AlphaFold3 使用扩散模型)。因此,系统理解这两类模型是一项非常有价值的能力。
这两类生成模型有一个共同特征:它们通过迭代地将噪声转化为数据来生成对象;这一“从噪声到数据”的演化过程,通常由常微分方程或随机微分方程(ODE/SDE)的数值模拟来实现。流匹配与去噪扩散模型可以看作一族方法:它们允许我们在深度神经网络的帮助下,大规模地构造、训练并模拟相应的 ODE/SDE。虽然实现上并不复杂,但由于 SDE 的技术性细节,理解这些模型往往并不容易。本课程将提供一套自洽的数学工具箱(尤其是微分方程相关内容),帮助你系统地理解这些模型背后的原理。
备注 1(补充资源,Additional Resources)
虽然本文笔记力求自洽,但仍推荐你配合以下两类资源一起学习:
- 课程录像(Lecture recordings):以讲授形式串联每一节内容;
- 实验课(Labs):指导你从零实现自己的扩散模型,强烈建议“动手写代码”。
以上资源可在课程主页获取:
https://diffusion.csail.mit.edu/。
1.2 课程结构(Course Structure)#
这里对本文档(课程笔记)的结构做一个简要导读:
- 第 1 节:采样视角下的生成式建模(Generative Modeling as Sampling):形式化“生成”的含义。我们把诸如“如何生成一张狗的图片?”这类问题,转化为更精确的数学问题——从某个概率分布中采样。
- 第 2 节:流与扩散模型(Flow and Diffusion Models):解释“如何生成”的机制。正如课程名所暗示,这套机制本质上是对常微分方程与随机微分方程(ODE/SDE)的数值模拟;我们会介绍微分方程的基本概念,并说明如何用神经网络来构造这些方程。
- 第 3 节:构建训练目标(Constructing a Training Target):训练生成模型前,必须先明确模型要逼近的“真值”到底是什么(ground truth)。我们将引入著名的福克–普朗克方程(Fokker–Planck equation),并推导训练目标的形式。
- 第 4 节:训练生成模型(Training the Generative Model):在给定训练目标后,说明如何训练神经网络以学习相应的 ODE/SDE。
- 第 5 节:构建图像生成器(Building an Image Generator):把前述理论落到具体的图像生成系统,包括引导(guidance)与常用网络架构等。
背景要求(Required background)
由于主题较为技术性,我们建议读者具备一定的数学基础,尤其是对概率论的基本概念有所了解。因此,原文在附录 A 中加入了概率论回顾(A Reminder on Probability Theory)。如果其中有些概念你暂时不熟悉也没关系:后续内容会反复用到它们,你可以按需回看。
1.3 采样视角下的生成式建模(Generative Modeling As Sampling)#
先从我们可能遇到的各种数据类型(或者称为模态,Modalities)以及如何用数字来表示它们开始:
图像(Image):考虑一幅具有 $H \times W$ 个像素的图像,其中 $H$ 为高、$W$ 为宽,每个像素包含三个颜色通道(RGB)。对每个像素与每个颜色通道,我们都有一个实数强度值。因此,一幅图像可表示为 $z \in \mathbb{R}^{H \times W \times 3}.$
视频(Video):视频就是随时间排列的一系列图像。若有 $T$ 个时间点或帧,则视频可表示为 $z \in \mathbb{R}^{T \times H \times W \times 3}.$
分子结构(Molecular Structure):一种朴素表示方式是用矩阵 $z=(z^1,\ldots,z^N)\in\mathbb{R}^{3\times N},$ 其中 $N$ 是分子中的原子数,每个 $z^i\in\mathbb{R}^3$ 描述该原子的空间位置。当然,还有更复杂的表示方式。
在以上所有例子中,我们要生成的对象在数学上都可以(在必要时展平后)表示为一个向量。因此,本文将采用如下约定:
核心要点 1(对象即向量,Objects as Vectors)
我们把要生成的对象视为向量 $z\in\mathbb{R}^d$。
一个值得注意的例外是文本数据。它通常被建模为离散对象,并通过自回归语言模型(Autoregressive Language Models,ARLMs,例如 ChatGPT)来处理。虽然已有针对离散数据的流模型(flow models)与扩散模型(Diffusion Models,DMs)等方法被发展出来,但本文仅聚焦于连续数据的应用。
将“生成”表述为“采样”(Generation as Sampling)#
让我们定义“生成”的含义。比如我们想生成“一张狗的图片”。显然,满足要求的图片有很多,并不存在唯一“最好”的那张。更贴切的说法是:存在一个对所有可能狗图像的概率分布。我们称它为数据分布(Data Distribution,$p_{\text{data}}$)。在狗图像的例子中,该分布会对“更像狗”的图像赋予更高的概率。因此,“好不好看”的主观描述可以被“在 $p_{\text{data}}$ 下的可能性有多大”所替代。于是,生成可以被数学化为从(未知的)分布 $p_{\text{data}}$ 采样。
核心要点 2(将生成视为采样,Generation as Sampling)
生成一个对象 $z$ 被建模为从数据分布中采样:$z \sim p_{\text{data}}$。
生成模型(Generative Model,GM)是一类机器学习模型,它允许我们从 $p_{\text{data}}$ 生成样本。在机器学习中,训练模型需要数据;在生成建模中,我们通常假设能获得一个有限的样本集合,这些样本独立同分布(Independent and Identically Distributed,i.i.d.)地来自 $p_{\text{data}}$,并共同作为真实分布的代理。
核心要点 3(数据集,Dataset)
一个数据集由有限个样本构成:$z_1,\ldots,z_N \stackrel{\text{i.i.d.}}{\sim} p_{\text{data}}$。
对于图像,我们可以通过整理互联网上公开可用的图片来构建数据集;对于视频,可以把 YouTube 作为数据库来使用;对于蛋白质结构,我们可以使用诸如蛋白质数据库(Protein Data Bank)等汇集了数十年科学测量的实验数据库。随着数据集规模的增大,它对底层分布 $p_{\text{data}}$ 的刻画会越来越充分。
条件生成(Conditional Generation)#
很多时候,我们希望在给定某些信息 $y$ 的条件下生成对象。例如,我们可能希望在条件 $y=$ “一条狗在被雪覆盖的山坡上奔跑,背景是群山”的描述下生成图像。我们可以把这改写为从一个条件分布采样:
核心要点 4(条件生成,Conditional Generation)
条件生成是从 $z \sim p_{\text{data}}(\cdot \mid y)$ 采样,其中 $y$ 是条件变量(conditioning variable)。
我们把 $p_{\text{data}}(\cdot \mid y)$ 称为条件数据分布(Conditional Data Distribution)。条件生成建模通常要求模型能够对任意而非固定的 $y$ 进行条件化。延续上面的例子,我们也可能希望在 $y=$ “一张写实风格的猫在吹生日蜡烛的图片”这样的文本提示下进行条件化。因此,我们希望有一个单一的模型,可以在任何给定的 $y$ 上进行条件化。事实证明,无条件生成的技术很容易推广到条件情形。于是,在前 3 个小节中,我们几乎只讨论无条件情形(同时牢记我们的目标是条件生成)。
从噪声到数据(From Noise to Data)#
到目前为止,我们讨论了生成建模的“是什么”:从 $p_{\text{data}}$ 生成样本。下面简要讨论“如何做”。我们假设可以从某个易于采样的初始分布(Initial Distribution,$p_{\text{init}}$)中取样,例如高斯分布$p_{\text{init}}=\mathcal{N}(0,I_d).$。生成建模的目标是把来自 $x \sim p_{\text{init}}$ 的样本变换成来自 $p_{\text{data}}$ 的样本。需要注意的是,$p_{\text{init}}$ 不一定必须是简单的高斯;我们将看到,利用更灵活的 $p_{\text{init}}$ 也有一些有趣的用例。尽管如此,在绝大多数应用中,我们仍将其取作简单的高斯分布,这一点需要牢记。
总结#
下面对本节内容做一小结。
总结 2(将生成视为采样,Summary 2)
我们对本节结论进行如下概括:
- 本文把要生成的对象视为向量 $z\in\mathbb{R}^d$,例如图像、视频或分子结构。
- 生成任务是在训练期间能够获取一个样本数据集 $z_1,\ldots,z_N \stackrel{\text{i.i.d.}}{\sim} p_{\text{data}}$ 的前提下,从概率分布 $p_{\text{data}}$ 生成样本。
- 条件生成假设我们在标签 $y$ 的条件下建模,并希望从 $p_{\text{data}}(\cdot\mid y)$ 采样;训练时可获得成对数据 $(z_1,y_1),\ldots,(z_N,y_N)$。
- 我们的目标是训练一个生成模型,将来自简单分布 $p_{\text{init}}$(例如高斯)的样本变换为来自 $p_{\text{data}}$ 的样本。
2 流与扩散模型(Flow and Diffusion Models)#
在上一节中,我们将生成式建模形式化为:从数据分布 $p_{\text{data}}$ 中采样。进一步地,我们看到采样可以通过把来自一个简单分布 $p_{\text{init}}$(例如高斯 $\mathcal{N}(0, I_d)$)的样本,变换为来自目标分布 $p_{\text{data}}$ 的样本来实现。本节描述:如何把所需的变换表示为某个恰当构造的微分方程的模拟。例如,流匹配与扩散模型分别涉及模拟常微分方程(Ordinary Differential Equations,ODEs)与随机微分方程(Stochastic Differential Equations,SDEs)。
本节的目标是定义并构造这些生成模型,并在后续部分中一直使用它们。具体做法是:先定义 ODE 与 SDE,并讨论它们的数值模拟;其次说明如何用深度神经网络参数化一个 ODE/SDE;这将引出流模型(flow model)与扩散模型(diffusion model)以及用于从这类模型中采样的基本算法;在后续章节中,我们再探讨如何训练这些模型。
2.1 流模型(Flow Models)#
![图 1:一个流 $\psi_t : \mathbb{R}^d \to \mathbb{R}^d$(红色方格网)由一个速度场 $u_t : \mathbb{R}^d \to \mathbb{R}^d$(用蓝色箭头表示)所定义,该速度场给出了在所有位置处的瞬时运动(这里 $d = 2$)。我们展示了三个不同的时间 $t$。可以看出,一个流是一个“扭曲”空间的微分同胚。图引自 [^15]。](/posts/mit-6.s184-%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/imgs/flow_1.png)
![图 1:一个流 $\psi_t : \mathbb{R}^d \to \mathbb{R}^d$(红色方格网)由一个速度场 $u_t : \mathbb{R}^d \to \mathbb{R}^d$(用蓝色箭头表示)所定义,该速度场给出了在所有位置处的瞬时运动(这里 $d = 2$)。我们展示了三个不同的时间 $t$。可以看出,一个流是一个“扭曲”空间的微分同胚。图引自 [^15]。](/posts/mit-6.s184-%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/imgs/flow_2.png)
![图 1:一个流 $\psi_t : \mathbb{R}^d \to \mathbb{R}^d$(红色方格网)由一个速度场 $u_t : \mathbb{R}^d \to \mathbb{R}^d$(用蓝色箭头表示)所定义,该速度场给出了在所有位置处的瞬时运动(这里 $d = 2$)。我们展示了三个不同的时间 $t$。可以看出,一个流是一个“扭曲”空间的微分同胚。图引自 [^15]。](/posts/mit-6.s184-%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/imgs/flow_3.png)
图 1:一个流 $\psi_t : \mathbb{R}^d \to \mathbb{R}^d$(红色方格网)由一个速度场 $u_t : \mathbb{R}^d \to \mathbb{R}^d$(用蓝色箭头表示)所定义,该速度场给出了在所有位置处的瞬时运动(这里 $d = 2$)。我们展示了三个不同的时间 $t$。可以看出,一个流是一个“扭曲”空间的微分同胚。图引自 [^15]。
我们从定义常微分方程(ODEs)开始。ODE 的解由一条轨迹(trajectory)给出,即一个函数
$$ X:[0,1]\to\mathbb{R}^d,\quad t\mapsto X_t, $$它把时间 $t$ 映射到空间 $\mathbb{R}^d$ 中的某个位置。每个 ODE 都由一个向量场(vector field) $u$ 定义,即
$$ u:\mathbb{R}^d\times[0,1]\to\mathbb{R}^d,\quad (x,t)\mapsto u_t(x), $$也就是说:对每个时间 $t$ 与位置 $x$,我们得到一个向量 $u_t(x)\in\mathbb{R}^d$,表示空间中的速度(见图 1)。ODE 对轨迹施加条件:我们希望一条轨迹 $X$ “沿着”向量场 $u_t$ 的方向,从点 $x_0$ 出发。形式化地,这样的轨迹是下面方程的解:
$$ \frac{d}{dt}X_t = u_t(X_t) \quad (1a)\quad\text{(ODE)} $$$$ X_0 = x_0 \quad (1b)\quad\text{(初始条件)} $$式(1a)要求:$X_t$ 的导数由 $u_t$ 指定的方向给出。式(1b)规定:在 $t=0$ 时从 $x_0$ 出发。
现在我们可以问:如果从 $t=0$ 起始于 $x_0$,那么在任一时刻 $t$(也即 $X_t$)会在哪里?这个问题由称为流(flow)的函数回答,它是 ODE 的一个解:
$$ \psi:\mathbb{R}^d\times[0,1]\to\mathbb{R}^d,\quad (x_0,t)\mapsto \psi_t(x_0) \quad (2a) $$$$ \frac{d}{dt}\,\psi_t(x_0)=u_t\!\big(\psi_t(x_0)\big) \quad (2b)\quad\text{(由向量场诱导的流的 ODE)} $$$$ \psi_0(x_0)=x_0 \quad (2c)\quad\text{(流的初始条件)} $$给定初始条件 $X_0=x_0$,ODE 的轨迹由 $X_t=\psi_t(X_0)$ 恢复。因此,向量场定义 ODE,而 ODE 的解即为流。
如同处理每个方程一样,我们应当问:ODE 的解是否存在?若存在是否唯一?在对 $u_t$ 施加较弱假设的情况下,数学中的一个基本结果给出了肯定答案:
定理 3(流的存在性与唯一性,Flow existence and uniqueness)
若 $u:\mathbb{R}^d\times[0,1]\to\mathbb{R}^d$ 连续可微且其导数有界,则(2)中的 ODE 存在唯一由流 $\psi_t$ 给出的解。在这种情况下,对所有 $t$,$\psi_t$ 是一个微分同胚(diffeomorphism),即 $\psi_t$ 连续可微且其逆映射 $\psi_t^{-1}$ 也连续可微。
在机器学习中,用神经网络来参数化 $u_t(x)$ 时,上述假设几乎总能满足(神经网络的导数有界)。因此,对我们感兴趣的情形来说,流存在且是 ODE 的唯一解。证明可见文献 1 2。
例 4(线性向量场,Linear Vector Fields)
考虑一个简单的向量场 $u_t(x)$,其在 $x$ 上为线性:$u_t(x)=-\theta x$,其中 $\theta>0$。则
$$\psi_t(x_0)=\exp(-\theta t)\,x_0 \quad (3)$$定义了一个解(流)并满足(2)。可直接验证:$\psi_0(x_0)=x_0$,且
$$ \frac{d}{dt}\psi_t(x_0)=\frac{d}{dt}\big(\exp(-\theta t)\,x_0\big)=-\theta \exp(-\theta t)\,x_0 =-\theta \psi_t(x_0)=u_t\!\big(\psi_t(x_0)\big), $$其中用到了链式法则。在图 3 中,我们可视化了该形式的流以指数方式收敛到 $0$。
模拟 ODE(Simulating an ODE)#
一般来说,如果 $u_t$ 并非像上述那样简单的线性函数,我们无法显式计算流 $\psi_t$。此时需使用数值方法来模拟 ODE。幸运的是,这是数值分析中的经典且研究充分的主题,已有大量强有力的方法 3。最简单、最直观的方法之一是欧拉方法(Euler method)。在欧拉方法中,从 $X_0=x_0$ 初始化,并按如下方式更新:
$$ X_{t+h}=X_t+h\,u_t(X_t)\qquad (t=0,h,2h,3h,\ldots,1-h) \quad (4) $$其中 $h=n^{-1}>0$ 是一个步长超参数(step size hyperparameter),$n\in\mathbb{N}$。在本课程中,欧拉方法已经足够。作为更复杂方法的示例,考虑海恩方法(Heun’s method),其更新规则为
$$ X_{t+h}'=X_t+h\,u_t(X_t)\quad\text{(新状态的初始猜测)} $$$$ X_{t+h}=X_t+\frac{h}{2}\Big(u_t(X_t)+u_{t+h}\big(X_{t+h}'\big)\Big)\quad\text{(用当前与猜测状态的平均方向修正)} $$直观地说,海恩方法先得到下一步的第一次猜测 $X_{t+h}'$,再利用修正后的平均方向给出更新。
流模型(Flow models)#
现在我们可以通过 ODE 构造一个生成模型。回忆我们的目标:把一个简单分布 $p_{\text{init}}$ 变换为一个复杂分布 $p_{\text{data}}$。因此,模拟 ODE 是实现该变换的自然选择。一个流模型由下面的 ODE 描述:
$$ X_0\sim p_{\text{init}}\quad\text{(随机初始化)} $$$$ \frac{d}{dt}X_t=u_t^{\theta}(X_t)\quad\text{(ODE)} $$其中向量场 $u_t^{\theta}$ 是带参数 $\theta$ 的神经网络(neural network)。目前,我们把 $u_t^{\theta}$ 视为一般的神经网络,即一个连续函数
$$ u_t^{\theta}:\mathbb{R}^d\times[0,1]\to\mathbb{R}^d $$(参数为 $\theta$)。稍后我们将讨论具体的网络结构选择。我们的目标是使轨迹的终点 $X_1$ 服从分布 $p_{\text{data}}$,即
$$ X_1\sim p_{\text{data}} \quad\Longleftrightarrow\quad \psi_1^{\theta}(X_0)\sim p_{\text{data}}, $$其中 $\psi_t^{\theta}$ 表示由 $u_t^{\theta}$ 诱导的流。需要注意:虽然称为流模型,但神经网络参数化的是向量场而非流本身。要计算该流,我们必须数值模拟该 ODE。算法 1 总结了用欧拉方法从流模型采样的过程。
输入:神经网络向量场 $u_t^{\theta}$,步数 $n$
- 设 $t=0$
- 设步长 $h=\frac{1}{n}$
- 采样 $X_0\sim p_{\text{init}}$
- 循环 $i=0,\ldots,n-1$(对应 $t=0,h,2h,\ldots,1-h$ 共 $n$ 次更新):
- $X_{t+h}=X_t+h\,u_t^{\theta}(X_t)$
- 更新 $t\leftarrow t+h$
- 返回 $X_t$(此时 $t=1$,也即 $X_t=X_1$)
2.2 扩散模型(Diffusion Models)#
随机微分方程(Stochastic Differential Equations,SDEs)把常微分方程(Ordinary Differential Equations,ODEs)的确定性轨迹扩展为随机轨迹。随机轨迹通常称为随机过程 $(X_t)_{0\le t\le 1}$,可表述为
- 对任意 $0\le t\le 1$,$X_t$ 是一个随机变量;
- $X:[0,1]\to\mathbb{R}^d,\quad t\mapsto X_t$ 是一次对 $X$ 的抽样得到的随机轨迹。
特别地,即使我们两次模拟同一个随机过程,结果也可能不同,因为其动力学被设计为随机的。
布朗运动(Brownian Motion,亦称 Wiener 过程)#
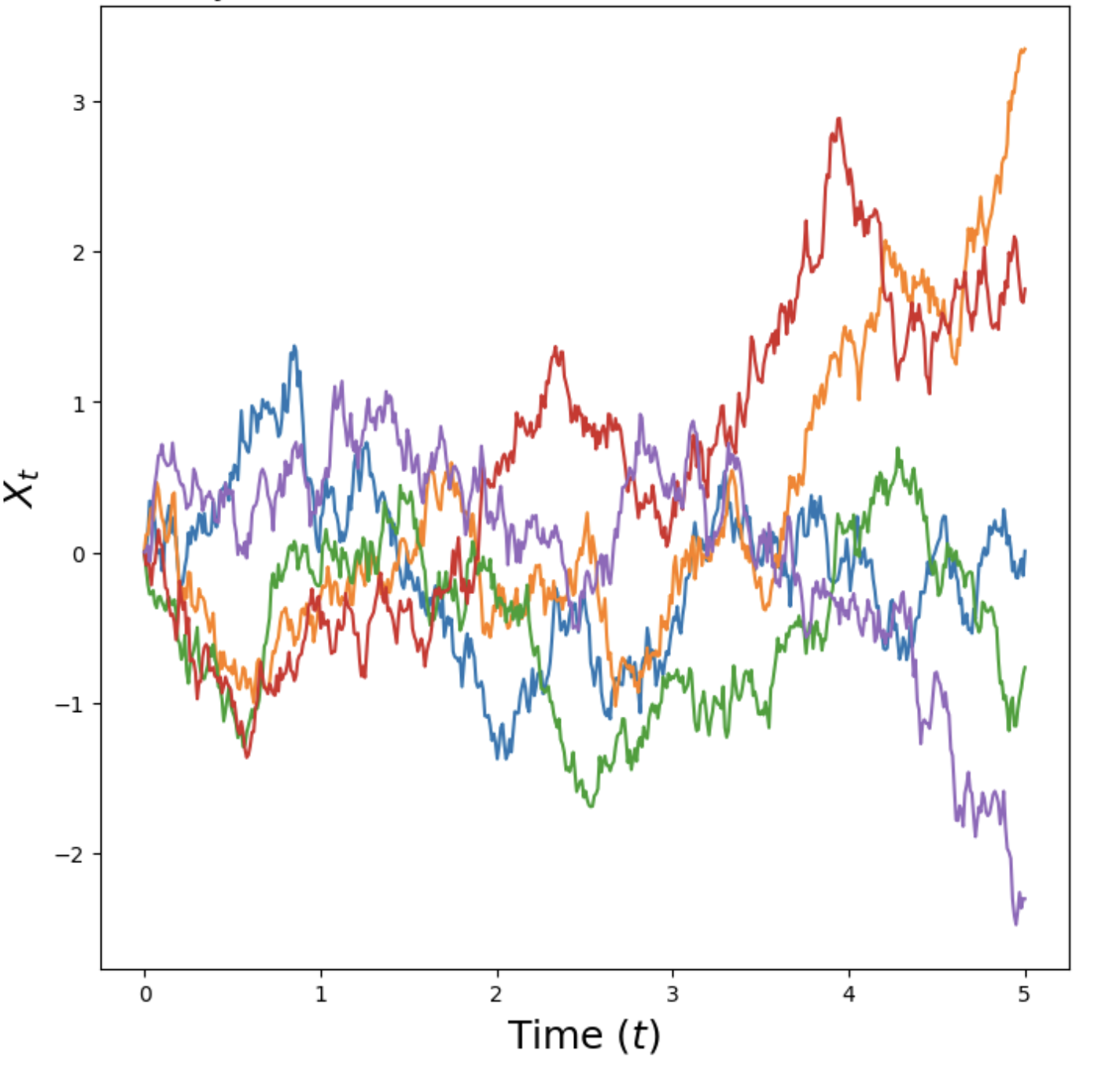
图 2:一维布朗运动 $(W_t)$ 的若干样本轨迹,使用式 (5) 进行模拟得到。
SDE 是通过布朗运动构造的——它是研究物理扩散过程时得到的一类基础随机过程。可以把布朗运动看作连续时间的随机游走。定义如下:布朗运动 $W=(W_t)_{0\le t\le 1}$ 满足 $W_0=0$,轨迹 $t\mapsto W_t$ 连续,并满足:
正态增量(Normal increments):对所有 $0\le s
独立增量(Independent increments):对任意 $0\le t_0
布朗运动又称 Wiener 过程,因此常用字母 “$W$” 记号。我们可以用步长 $h>0$ 的近似更新来模拟布朗运动:令 $W_0=0$,然后
$$ W_{t+h}=W_t+\sqrt{h}\,\varepsilon_t,\quad \varepsilon_t\sim\mathcal{N}(0,I_d),\quad t=0,h,2h,\ldots,1-h \quad (5) $$直观地说,布朗运动之于随机过程理论,就像高斯分布之于概率分布理论一样核心。从金融到统计物理再到流行病学,布朗运动的研究在机器学习之外也有广泛应用:在金融中,它常用于刻画复杂金融工具的价格。此外,作为一种数学构造,布朗运动也颇具魅力——其路径处处连续(你可以不抬笔一直画下去),却也无限长(因此永远画不完)。
从 ODE 到 SDE(From ODEs to SDEs)#
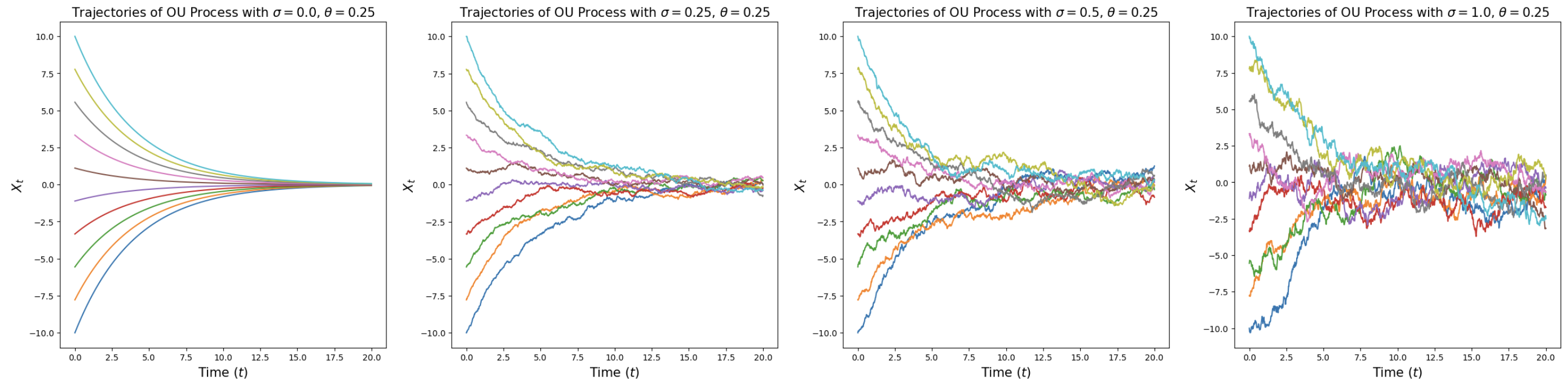
图 3:一维 Ornstein–Uhlenbeck 过程(见公式 (8))的示意图,其中 $\theta=0.25$,$\sigma$ 取不同的数值(从左到右递增)。当 $\sigma=0$ 时,我们得到的是一个流(光滑的、确定性的轨迹),其在 $t\to\infty$ 时收敛到原点。对于 $\sigma>0$,得到的是随机路径,它们在 $t\to\infty$ 时收敛到高斯分布 $\mathcal{N}(0,\sigma^2/2\theta)$。
SDE 的思想:在 ODE 的确定性动力学上,叠加由布朗运动驱动的随机动力学。由于一切都是随机的,我们不能再像式 (1a) 那样直接取导数,因此需要给出不显式用导数的等价表述。对 ODE 的轨迹 $(X_t)_{0\le t\le 1}$,有
$$ \begin{aligned} \frac{d}{dt}X_t &= u_t(X_t) &&\qquad \text{(经由导数的表达式)} \\[2pt] \overset{(i)}{\iff}\ \frac{1}{h}\bigl(X_{t+h}-X_t\bigr) &= u_t(X_t)+R_t(h) \\[2pt] \iff\ X_{t+h} &= X_t + h\,u_t(X_t) + h\,R_t(h) &&\qquad \text{(经由无穷小更新的表达式)} \end{aligned} $$其中 $(i)$ 处使用了导数的定义,$R_t(h)$ 是当 $h$ 足够小时可忽略的误差项,满足 $\lim_{h\to 0}R_t(h)=0$。上述推导仅重申:ODE 的轨迹在每个时间步沿着向量场 $u_t(X_t)$ 做一个小步。
现在把它随机化:令每一步不仅有确定性项 $u_t(X_t)$,还叠加来自布朗运动的贡献,则
$$ X_{t+h} = X_t + \underbrace{h u_t(X_t)}_{\text{确定项}} + \underbrace{\sigma_t (W_{t+h} - W_t)}_{\text{随机项}} + \underbrace{h R_t(h)}_{\text{误差项}} \quad (6) $$其中 $\sigma_t\ge 0$ 为扩散系数(Diffusion Coefficient),$R_t(h)$ 为随机误差项,当 $h\to 0$时满足,$\mathbb{E}\!\left[\lVert R_t(h)\rVert_2^2\right]^{1/2}\to 0$ 。
这就是随机微分方程(SDE),常用下面的符号式(仅作记号,等价于式 (6))表示:
$$ dX_t = u_t(X_t)\,dt + \sigma_t\,dW_t \quad (7a)\quad\text{(SDE)} $$$$ X_0 = x_0 \quad (7b)\quad\text{(初始条件)} $$需要牢记:上述 $dX_t$ 只是对式 (6) 的非严格写法。与 ODEs 不同,SDEs 一般没有流映射(Flow Map,$\phi_t$),因为 $X_t$ 的取值不仅由初值 $X_0\sim p_{\text{init}}$ 决定,演化本身也是随机的。
定理 5(SDE 的解的存在与唯一性,SDE Solution Existence and Uniqueness)
若 $u:\mathbb{R}^d\times[0,1]\to\mathbb{R}^d$ 连续可微且导数有界,并且 $\sigma_t$ 连续,则 (7) 所给的 SDE 存在唯一的解过程 $(X_t)_{0\le t\le 1}$,其满足式 (6)。
这是随机分析课程中的核心结果,需要通过构造布朗运动与随机积分来严格证明。本文聚焦于机器学习应用,技术细节参见文献 4。另外,任何 ODE 也可视为特殊的 SDE(取 $\sigma_t=0$)。因此下文谈到 SDEs 时,默认 ODEs 是它的特例。
例 6(Ornstein–Uhlenbeck Process,OU 过程)
取常数扩散系数 $\sigma_t=\sigma\ge 0$ 与常线性漂移 $u_t(x)=-\theta x\ (\theta>0)$,得到
$$dX_t=-\theta X_t\,dt+\sigma\,dW_t \quad (8)$$其解称为 OU 过程。向量场 $-\theta x$ 把过程拉回中心 $0$,而扩散系数 $\sigma$ 持续注入噪声。若模拟到 $t\to\infty$,分布收敛到 $\mathcal{N}\!\left(0,\sigma^2 / 2\theta\right)$。当 $\sigma=0$ 时,退化为我们在式 (3) 中研究过的线性流。
模拟 SDE(Simulating an SDE)#
若目前对 SDE 的抽象定义不够直观,可以直接从“如何数值模拟 SDE”来理解。最简单的方法是 Euler–Maruyama 方法(EM 法),它之于 SDE,正如欧拉法之于 ODE。用 EM 法,从 $X_0=x_0$ 出发迭代:
$$ X_{t+h}=X_t+h\,u_t(X_t)+\sqrt{h}\,\sigma_t\,\varepsilon_t,\quad \varepsilon_t\sim\mathcal{N}(0,I_d), \quad (9) $$其中 $h=n^{-1}>0$ 为步长超参数($n\in\mathbb{N}$)。也就是说,每一步沿 $u_t(X_t)$ 前进一小步,并加入尺度为 $\sqrt{h}\sigma_t$ 的高斯噪声。本文及配套实验中,默认采用 EM 法来模拟 SDE。
扩散模型(Diffusion Models,DMs)#
我们可以像在 ODE 情形那样,用 SDE 构造生成模型:目标是把简单分布 $p_{\text{init}}$ 逐步变换为复杂的数据分布 $p_{\text{data}}$。与 ODE 相同,取 $X_0\sim p_{\text{init}}$ 并按某个 SDE 演化是自然选择。参数化上,只需参数化关键成分——向量场 $u_t$,例如用神经网络表示。
输入:神经网络 $u_t^\theta$,步数 $n$,扩散系数 $\sigma_t$
- 设 $t=0$
- 设步长 $h=1/n$
- 采样 $X_0\sim p_{\text{init}}$
- 循环 $i=0,\ldots,n-1$(对应 $t=0,h,2h,\ldots,1-h$ 共 $n$ 次更新):
- 采样 $\varepsilon\sim\mathcal{N}(0,I_d)$
- 更新 $X_{t+h}=X_t+h\,u_t^\theta(X_t)+\sigma_t\sqrt{h}\,\varepsilon$
- 更新 $t\leftarrow t+h$
- 返回 $X_t$(此时 $t=1$,也即 $X_t=X_1$)
因此,一个扩散模型可写为
$$ dX_t=u_t^\theta(X_t)\,dt+\sigma_t\,dW_t \quad\text{(SDE)} $$$$ X_0\sim p_{\text{init}} \quad\text{(随机初始化)} $$总结 7(基于 SDE 的生成模型,SDE generative model)
在本文中,扩散模型(DM)由参数为 $\theta$ 的神经网络 $u_t^\theta$(参数化向量场)与固定的扩散系数 $\sigma_t$ 组成:
- 神经网络:$u^\theta:\mathbb{R}^d\times[0,1]\to\mathbb{R}^d,\ (x,t)\mapsto u_t^\theta(x)$;
- 固定项:$\sigma_t:[0,1]\to[0,\infty),\ t\mapsto\sigma_t$。
获得模型样本(即生成对象)的流程:
- 初始化:$X_0\sim p_{\text{init}}\quad\text{(用简单分布随机初始化,如高斯)}$;
- 模拟:$dX_t=u_t^\theta(X_t)\,dt+\sigma_t\,dW_t\quad\text{(SDE 从 0 演化到 1)}$;
- 目标:$X_1\sim p_{\text{data}}\quad\text{(使最终分布接近数据分布)}$。
当 $\sigma_t=0$ 时,扩散模型退化为流模型(Flow Model)。
3 构建训练目标(Constructing the Training Target)#
在上一节中,我们构造了流模型(Flow model)和扩散模型(Diffusion model),它们通过模拟如下的常微分方程(Ordinary Differential Equation,ODE)/ 随机微分方程(Stochastic Differential Equation,SDE)得到轨迹 $(X_t)_{0\le t\le 1}$:
$$ X_0\sim p_{\text{init}},\quad \mathrm{d}X_t=u_t^\theta(X_t)\,\mathrm{d}t \quad (10)\ \qquad\text{(流模型)} $$$$ X_0\sim p_{\text{init}},\quad \mathrm{d}X_t=u_t^\theta(X_t)\,\mathrm{d}t+\sigma_t\,\mathrm{d}W_t \quad (11)\ \qquad\text{(扩散模型)} $$其中,$u_t^\theta$ 是一个神经网络,$\sigma_t$ 为固定的扩散系数。显然,如果我们随机初始化神经网络的参数 $\theta$,直接模拟 ODE/SDE 得到的只是“噪声”。和常规机器学习一样,我们需要训练这个神经网络。我们通过最小化诸如均方误差(mean-squared error,MSE)的损失函数 $ \mathcal{L}(\theta)$ 来实现这一点:
$$ \mathcal{L}(\theta) = \| u_t^{\theta}(x) - \underbrace{u_t^{\text{target}}(x)}_{\text{训练目标}} \|^2, $$其中 $u_t^{\text{target}}(x)$ 是我们希望逼近的训练目标(training target)。为了推导训练算法,我们分两步进行:本章的目标是找到训练目标 $u_t^{\text{target}}$ 的解析表达式;下一章我们会描述近似这个训练目标的训练算法。由于 $u_t^\theta$ 是向量场网络,训练目标 $u_t^{\text{target}}: \mathbb{R}^d\times [0,1]\to \mathbb{R}^d$ 也应当是一个向量场;此外,$u_t^{\text{target}}$ 应当实现我们期望 $u_t^\theta$ 实现的功能:把噪声转换为数据。因此,本章的目标是推导训练目标 $u_t^{\text{target}}$ 的公式,使得对应的 ODE/SDE 能够把 $p_{\text{init}}$ 转换为 $p_{\text{data}}$。在此过程中,我们会遇到两个源自物理与随机分析的基本结果:连续性方程(Continuity Equation)与福克-普朗克方程(Fokker–Planck Equation)。我们先从 ODE 的关键思想讲起,然后再推广到 SDE。
备注 8(Remark 8)
推导 Flow 与 Diffusion 模型训练目标的方法有很多。本节给出的做法既通用又相对简单,并且与近期的 SOTA 模型一致。尽管与某些扩散模型的既有叙述不同,但稍后我们也会讨论替代的表述方式。

图 4:通过高斯条件概率路径,在一组图像上实现从噪声到数据的逐步插值。
3.1 条件与边缘概率路径(Conditional and Marginal Probability Path)#
构造训练目标 $u_t^{\text{target}}$ 的第一步是指定一个概率路径(Probability Path)。直观地说,概率路径刻画了在 $p_{\text{init}}$ 与 $p_{\text{data}}$ 之间的逐渐插值。在本小节我们给出其构造方法。对一个数据点 $z\in\mathbb{R}^d$,我们用 $\delta_z$ 表示狄拉克 delta(Dirac delta)“分布”。条件(插值)概率路径(Conditional (interpolation) Probability Path)是指满足下式的一组分布 $p_t(x|z)$:
$$ p_0(\cdot|z)=p_{\text{init}},\quad p_1(\cdot|z)=\delta_z,\quad \forall\,z\in\mathbb{R}^d. \quad (12) $$换言之,条件概率路径把单个数据点逐步转换为初始分布(参见图示)。你可以把概率路径想象为“分布空间中的一条轨迹”。每个条件概率路径 $p_t(x|z)$ 都诱导出一个边缘概率路径(Marginal Probability Path) $p_t(x)$,其定义为:先从数据分布中采样 $z\sim p_{\text{data}}$,再从 $p_t(\cdot|z)$ 采样:
$$ z\sim p_{\text{data}},\quad x\sim p_t(\cdot|z)\ \Longrightarrow\ x\sim p_t \quad (13)\qquad\text{(从边缘概率路径采样)} $$$$ p_t(x)=\int p_t(x|z)\,p_{\text{data}}(z)\,\mathrm{d}z. \quad (14)\qquad\text{(边缘概率路径的密度)} $$需要注意,我们会采样 $p_t$,但由于积分常常不可解,我们并不知道显式的密度函数 $p_t(x)$。由式 (12) 可知,该边缘概率路径在 $p_{\text{init}}$ 与 $p_{\text{data}}$ 之间插值:
$$ p_0=p_{\text{init}},\quad p_1=p_{\text{data}}. \quad (15)\qquad\text{(噪声–数据插值)} $$例 9(Example 9:Gaussian Conditional Probability Path,高斯条件概率路径)
一个特别常用的概率路径是高斯概率路径(Gaussian probability path),这正是去噪扩散模型(denoising diffusion models,DDMs)所采用的路径。令 $\alpha_t,\beta_t$ 为噪声调度器(noise schedulers):两条连续可微、单调的函数,满足 $\alpha_0=\beta_1=0$ 与 $\alpha_1=\beta_0=1$。定义
$$p_t(\cdot|z)=\mathcal{N}(\alpha_t z,\ \beta_t^2 I_d) \quad (16)\qquad\text{(高斯条件路径)}$$由上述条件可得
$$ p_0(\cdot|z)=\mathcal{N}(\alpha_0 z,\beta_0^2 I_d)=\mathcal{N}(0,I_d),\quad p_1(\cdot|z)=\mathcal{N}(\alpha_1 z,\beta_1^2 I_d)=\delta_z $$因此该 $p_t(x|z)$ 满足式 (12)(在 $p_{\text{init}}=\mathcal{N}(0,I_d)$ 的情形下)并构成有效的条件插值路径。高斯条件概率路径拥有许多良好性质,尤为适合我们的目标,因此我们会把它作为贯穿本章的“原型”。
由该条件路径得到的边缘高斯路径可按如下方式采样:
$$ z\sim p*{\text{data}},\quad \varepsilon\sim p*{\text{init}}=\mathcal{N}(0,I_d) \ \Longrightarrow\ x=\alpha_t z+\beta_t\varepsilon \sim p_t. \quad (17) $$直觉上,$t$ 越小,加入的噪声越多;当 $t=0$ 时只剩噪声。图示展示了在高斯噪声与简单数据分布之间插值的一个例子。
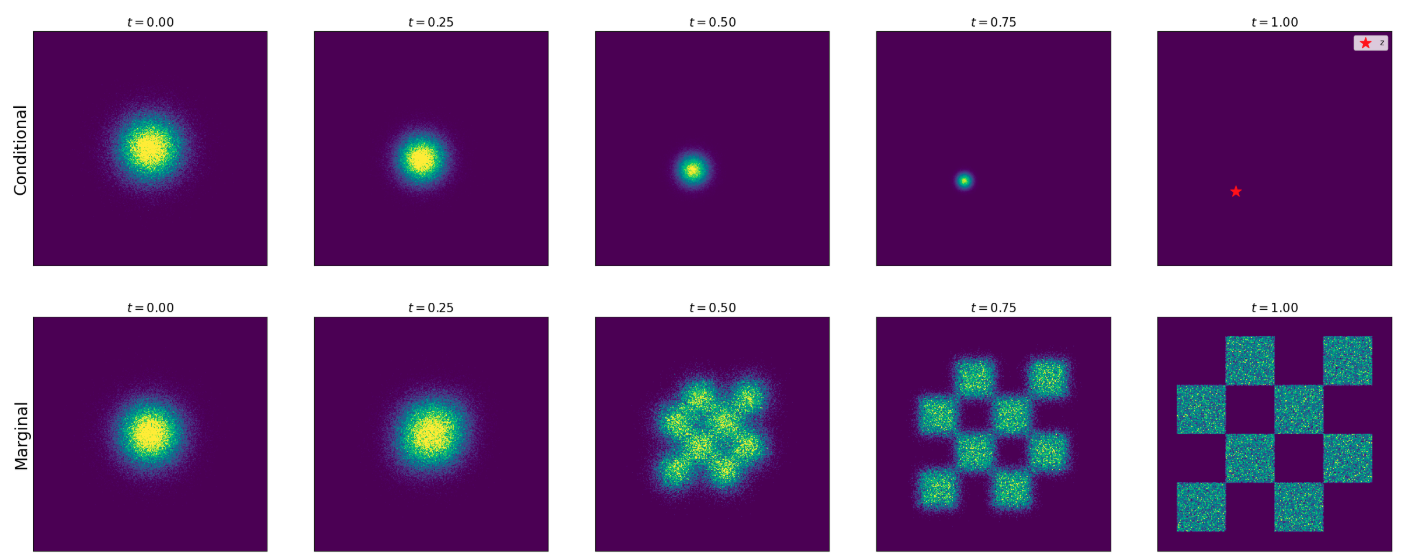
图 5:条件(上部)和边缘(下部)概率路径的示意图。这里我们绘制了一个高斯概率路径,其中 $\alpha_t=t$,$\beta_t=1-t$。条件概率路径在单个数据点 $z$ 的情形下,在高斯分布 $p_{\text{init}}=\mathcal{N}(0,I*d)$ 和 $p*{\text{data}}=\delta*z$ 之间进行插值。边缘概率路径在一个高斯分布与数据分布 $p*{\text{data}}$ 之间插值(这里,$p_{\text{data}}$ 是一个二维玩具分布,用棋盘格图案表示)。
3.2 条件与边缘向量场(Conditional and Marginal Vector Fields)#
接下来我们基于刚定义的概率路径 $p_t$ 为 流模型构造训练目标 $u_t^{\text{target}}$。思想是先构造条件向量场(Conditional Vector Field),再由此得到边缘向量场(Marginal Vector Field)。
定理 10(Theorem 10:Marginalization trick,边缘化技巧)
对任意数据点 $z\in\mathbb{R}^d$,令 $u_t^{\text{target}}(\cdot|z)$ 表示一个条件向量场,它的 ODE 轨迹满足下式,从而对应的分布即为条件概率路径 $p_t(\cdot|z)$:
$$ X*0\sim p*{\text{init}},\quad \frac{\mathrm{d}}{\mathrm{d}t}X_t=u_t^{\text{target}}(X_t\mid z)\ \Longrightarrow\ X_t\sim p_t(\cdot\mid z),\quad (0\le t\le 1). \quad (18) $$定义边缘向量场
$$ u*t^{\text{target}}(x)=\int u_t^{\text{target}}(x\mid z)\, \frac{p_t(x\mid z)\,p*{\text{data}}(z)}{p_t(x)}\,\mathrm{d}z. \quad (19) $$则该向量场所诱导的边缘路径满足
$$ X*0\sim p*{\text{init}},\quad \frac{\mathrm{d}}{\mathrm{d}t}X_t=u_t^{\text{target}}(X_t) \ \Longrightarrow\ X_t\sim p_t,\quad (0\le t\le 1). \quad (20) $$特别地,对该 ODE 有 $X_1\sim p_{\text{data}}$,因此可称 “$u_t^{\text{target}}$ 将噪声 $p_{\text{init}}$ 转换为数据 $p_{\text{data}}$”。
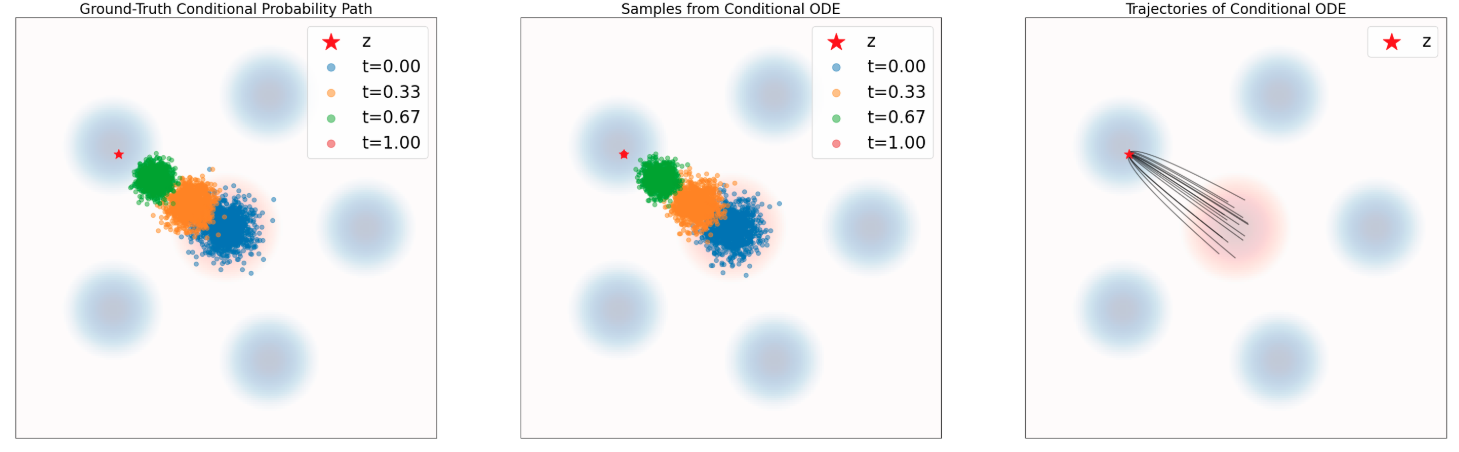
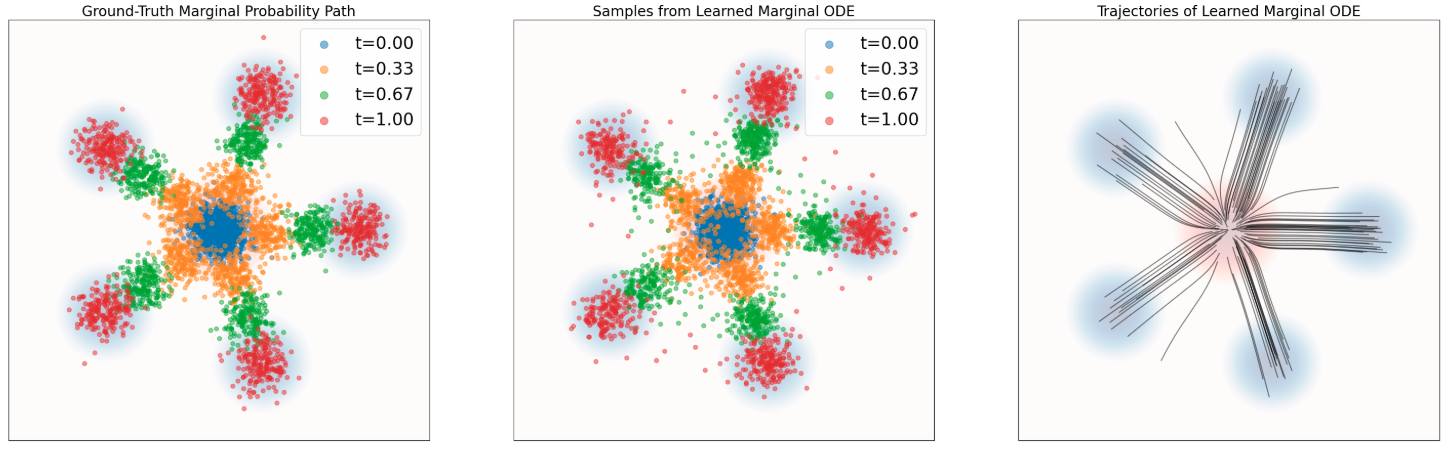
图 6:定理 10 的示意图。使用常微分方程(ODE)模拟一个概率路径。蓝色背景表示数据分布 $p_{\text{data}}$,红色背景表示高斯分布 $p_{\text{init}}$。上排:条件概率路径。左:来自条件路径 $p_t(\cdot\mid z)$ 的真实样本。中:随时间演化的 ODE 采样结果。右:使用式 (21) 中的目标向量场 $u_t^{\text{target}}(x\mid z)$ 模拟 ODE 所得到的轨迹。下排:模拟一个边缘概率路径。左:来自 $p_t$ 的真实样本。中:随时间演化的 ODE 采样结果。右:使用边缘向量场 $u_t^{\text{target}}(x)$ 模拟 ODE 所得到的轨迹。可以看到,条件向量场遵循条件概率路径,而边缘向量场遵循边缘概率路径。
在证明边缘化技巧之前,先说明它为何有用:定理 10 给出的边缘化技巧能把一个条件向量场(Conditional Vector Field)构造成一个边缘向量场(Marginal Vector Field)。这大大简化了求训练目标公式的问题,因为我们常常可以手工(也就是只做一些代数运算)找到一个满足式 (18) 的条件向量场 $u_t^{\text{target}}(\cdot\mid z)$。为说明这一点,下面以我们贯穿全章的高斯分布路径为例,推导一个条件向量场 $u_t(x\mid z)$。
例 11(Example 11:Target ODE for Gaussian probability paths,高斯概率路径的训练目标 ODE)
仍取 $p_t(\cdot|z)=\mathcal{N}(\alpha_t z,\beta_t^2 I_d)$,并记 $\dot{\alpha}_t=\partial_t\alpha_t,\ \dot{\beta}_t=\partial_t\beta_t$。我们要证明下面的条件高斯向量场(conditional Gaussian vector field)是定理 10 意义下的有效 CVF:
$$u_t^{\text{target}}(x|z)=\Bigl(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\Bigr)z+\frac{\dot{\beta}_t}{\beta_t}x. \quad (21)$$证明. 先构造条件流 $\psi_t^{\text{target}}(x|z)$:
$$\psi_t^{\text{target}}(x|z)=\alpha_t z+\beta_t x. \quad (22)$$若 $X_t$ 是该流的 ODE 轨迹,且 $X_0\sim p_{\text{init}}=\mathcal{N}(0,I_d)$,则
$$X_t=\psi_t^{\text{target}}(X_0|z)=\alpha_t z+\beta_t X_0\sim\mathcal{N}(\alpha_t z,\beta_t^2 I_d)=p_t(\cdot|z).$$因而轨迹分布即为条件概率路径(满足式 (18))。由流的定义,有
$$\frac{\mathrm{d}}{\mathrm{d}t}\psi_t^{\text{target}}(x|z)=u_t^{\text{target}}\bigl(\psi_t^{\text{target}}(x|z)\big|z\bigr),$$即
$$\dot{\alpha}_t z+\dot{\beta}_t x=u_t^{\text{target}}(\alpha_t z+\beta_t x|z),$$把变量重参数化为 $x\to(x-\alpha_t z)/\beta_t$,整理得
$$u_t^{\text{target}}(x|z)=\Bigl(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\Bigr)z+\frac{\dot{\beta}_t}{\beta_t}x,$$即式 (21)。
(也可把式 (21) 直接代入下述连续性方程来核对。)
为阐述后续内容,我们需要散度(divergence,div)算子。对向量场 $v_t$,定义
$$ \mathrm{div}(v_t)(x)=\sum_{i=1}^d\frac{\partial}{\partial x_i}v_t(x). \quad (23) $$定理 12(Theorem 12:Continuity Equation,连续性方程)
设 ODE 的向量场为 $u_t^{\text{target}}$ 且 $X_0\sim p_{\text{init}}$。则 $X_t\sim p_t\ (0\le t\le 1)$ 当且仅当
$$ \partial_t p_t(x)=-\,\mathrm{div}\!\bigl(p_t u_t^{\text{target}}\bigr)(x), \qquad \forall x\in\mathbb{R}^d,\ 0\le t\le 1. \quad (24) $$连续性方程描述了密度 $p_t(x)$ 随时间的变化率。直观地,$-\mathrm{div}(p_t u_t)$ 衡量了从向量场中“流入”的概率质量。总概率质量守恒使得两边相等。
用连续性方程证明定理 10. 只需证明按式 (19) 定义的 $u_t^{\text{target}}$ 满足式 (24):
$$ \begin{aligned} \partial_t p_t(x)\ &\stackrel{(i)}{=}\ \partial_t \int p_t(x|z)p_{\text{data}}(z)\,\mathrm{d}z \\ &\stackrel{(ii)}{=}\ \int \partial_t p_t(x|z)p_{\text{data}}(z)\,\mathrm{d}z \\ &\stackrel{(iii)}{=}\ \int\! \bigl[-\mathrm{div}\bigl(p_t(\cdot|z)u_t^{\text{target}}(\cdot|z)\bigr)(x)\bigr]\,p_{\text{data}}(z)\,\mathrm{d}z \\ &\stackrel{(iv)}{=}\ -\,\mathrm{div}\!\left(\int p_t(x|z)u_t^{\text{target}}(x|z)p_{\text{data}}(z)\,\mathrm{d}z\right) \\ &=\ -\,\mathrm{div}\!\left(p_t(x)\int u_t^{\text{target}}(x|z)\frac{p_t(x|z)p_{\text{data}}(z)}{p_t(x)}\,\mathrm{d}z\right) \\ &\stackrel{(v)}{=}\ -\,\mathrm{div}\bigl(p_t u_t^{\text{target}}\bigr)(x), \end{aligned} $$其中 $(i)$ 用到式 (13),$(ii)$ 交换时间导数与积分,$(iii)$ 为条件路径的连续性方程,$(iv)$ 交换积分与散度并“乘除”$p_t(x)$,$(v)$ 用到式 (19)。由定理 12 即得式 (20)。
3.3 条件与边缘得分函数(Conditional and Marginal Score Functions)#
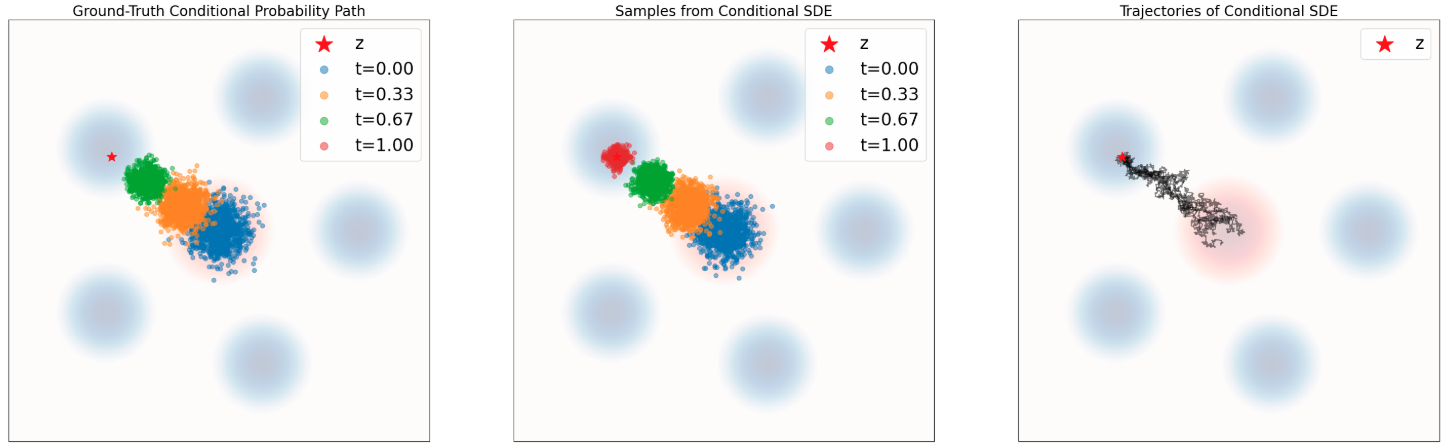
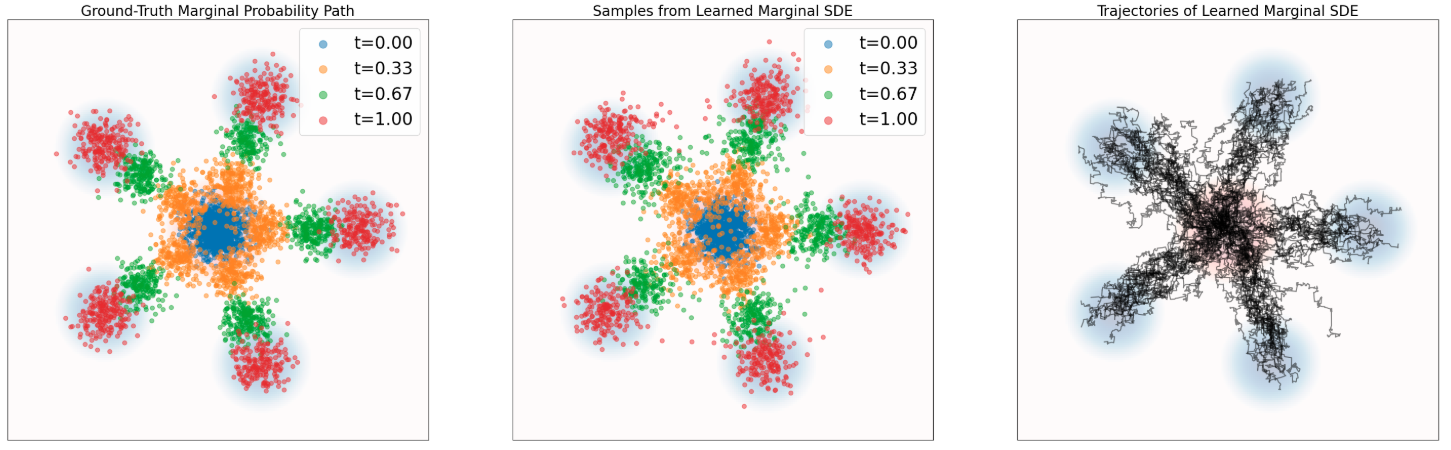
图 7:定理 13 的示意图。使用随机微分方程(SDE)来模拟一个概率路径。这里使用式 (25) 的 SDE 采样,重复了图 6 中的作图方式。蓝色背景表示数据分布 $p_{\text{data}}$,红色背景表示高斯分布 $p_{\text{init}}$。上排:条件路径。下排:边缘概率路径。可以看到,SDE 将来自 $p_{\text{init}}$ 的样本传输为来自 $\delta_z$ 的样本(对应条件路径),以及来自 $p_{\text{data}}$ 的样本(对应边缘路径)。
我们已经为流构造出了训练目标。现在把该思路扩展到 SDE。首先定义概率路径 $p_t$ 的边缘得分函数(marginal score function)为 $\nabla\log p_t(x)$,并据此把 ODE 扩展到 SDE:
定理 13(Theorem 13:SDE extension trick,SDE 扩展技巧)
仍按前述定义条件与边缘向量场 $u_t^{\text{target}}(\cdot|z),\,u_t^{\text{target}}(x)$。令扩散系数 $\sigma_t\ge 0$。考虑如下 SDE:
$$ X*0\sim p*{\text{init}},\quad \mathrm{d}X_t=\Bigl[u_t^{\text{target}}(X_t)+\frac{\sigma_t^2}{2}\nabla\log p_t(X_t)\Bigr]\mathrm{d}t+\sigma_t\,\mathrm{d}W_t. \quad (25) $$则其边缘分布满足
$$X_t\sim p_t,\quad (0\le t\le 1). \quad (26)$$同样的结论对条件版本也成立:把 $p_t(x)$ 与 $u_t^{\text{target}}(x)$ 分别替换为 $p_t(x|z)$ 与 $u_t^{\text{target}}(x|z)$ 亦然。
定理 13 中的公式很有用,因为与之前类似,我们可以通过条件得分函数(conditional score function)$\nabla \log p_t(x\mid z)$ 来表达边缘得分函数(marginal score function):
$$ \nabla \log p_t(x) = \frac{\nabla p_t(x)}{p_t(x)} = \frac{\nabla \int p_t(x\mid z)\,p_{\text{data}}(z)\,dz}{p_t(x)} = \frac{\int \nabla p_t(x\mid z)\,p_{\text{data}}(z)\,dz}{p_t(x)} = \int \nabla \log p_t(x\mid z)\,\frac{p_t(x\mid z)\,p_{\text{data}}(z)}{p_t(x)}\,dz. $$并且条件得分函数 $\nabla \log p_t(x\mid z)$ 通常可以解析地给出,下例即为说明。
例 14(Example 14:Score Function for Gaussian Probability Paths,高斯概率路径的得分函数)
对于高斯概率路径(Gaussian Probability Paths)$p_t(x\mid z)=\mathcal N\!\left(x;\,\alpha_t z,\beta_t^{2}I_d\right)$,利用高斯概率密度的形式(见式 (81))可得
$$ \nabla \log p_t(x\mid z) = \nabla \log \mathcal N\!\left(x;\,\alpha_t z,\beta_t^{2}I_d\right) = -\,\frac{x-\alpha_t z}{\beta_t^{2}}. $$注意:该得分关于 $x$ 为线性函数。这是高斯分布的一个独特性质。
在本节的其余部分,我们将通过福克–普朗克方程(Fokker–Planck equation,FPE)证明定理 13。该方程把连续性方程(continuity equation)从常微分方程(Ordinary Differential Equations)推广到随机微分方程(Stochastic Differential Equations)。为此,先定义拉普拉斯算子(Laplacian,$\Delta$),并约定梯度(gradient,$\nabla$)与散度(divergence,div)运算符如下:
$$ \Delta w_t(x) = \sum_{i=1}^{d}\frac{\partial^{2}}{\partial^{2}x_i}\,w_t(x) = \mathrm{div}(\nabla w_t)(x). \quad (29) $$定理 15(Theorem 15:Fokker–Planck Equation,福克-普朗克方程)
设 $p_t$ 为一条概率路径,并考虑 SDE
$$ X*0\sim p*{\text{init}},\qquad \mathrm{d}X_t=u_t(X_t)\,\mathrm{d}t+\sigma_t\,\mathrm{d}W_t. $$当且仅当
$$ \partial_t p_t(x)=-\,\mathrm{div}\!\bigl(p_t u_t\bigr)(x)+\frac{\sigma_t^2}{2}\Delta p_t(x), \qquad \forall x\in\mathbb{R}^d,\ 0\le t\le 1, \quad (30) $$有 $X_t\sim p_t\ (0\le t\le 1)$。
当 $\sigma_t=0$ 时,式 (30) 退化为连续性方程。$\Delta p_t$ 一项可视为“热扩散”,因此这也是热方程的推广形式。
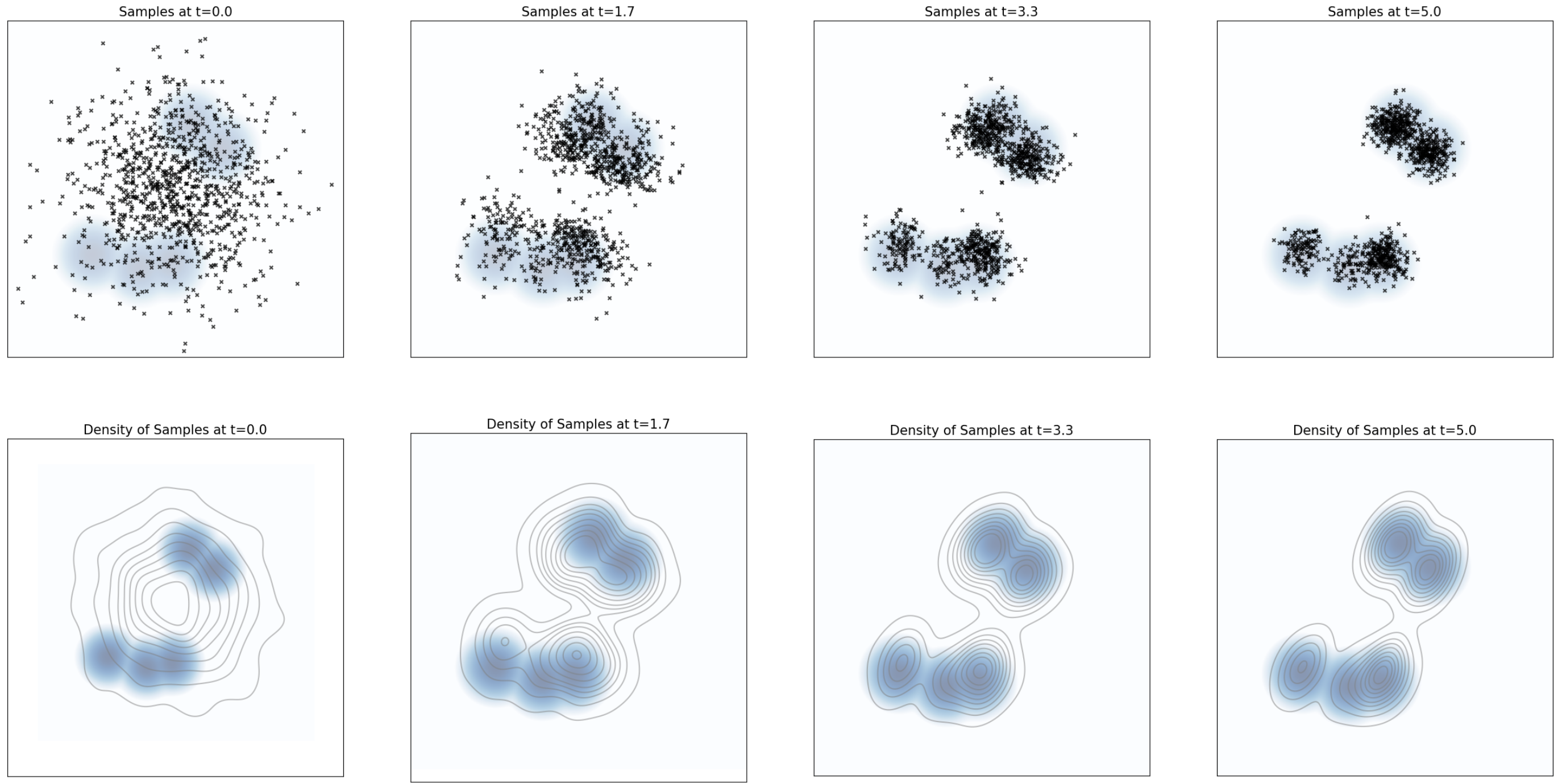
图 8:上排:粒子在由公式 (31) 给出的朗之万动力学下演化,此时 $p(x)$ 取为具有 5 个模态的高斯混合分布。下排:对上排中相同样本的核密度估计。可以看到,样本分布收敛到平衡分布 $p$(蓝色背景)。
用 FPE 证明定理 13. 对式 (25) 的漂移项,验证其满足式 (30):
$$ \begin{aligned} \partial_t p_t(x) &\stackrel{(i)}{=}\ -\,\mathrm{div}\!\bigl(p_t u_t^{\text{target}}\bigr)(x) \\ &\stackrel{(ii)}{=}\ -\,\mathrm{div}\!\bigl(p_t u_t^{\text{target}}\bigr)(x)-\frac{\sigma_t^2}{2}\Delta p_t(x)+\frac{\sigma_t^2}{2}\Delta p_t(x) \\ &\stackrel{(iii)}{=}\ -\,\mathrm{div}\!\bigl(p_t u_t^{\text{target}}\bigr)(x)-\mathrm{div}\!\Bigl(\frac{\sigma_t^2}{2}\nabla p_t(x)\Bigr)+\frac{\sigma_t^2}{2}\Delta p_t(x) \\ &\stackrel{(iv)}{=}\ -\,\mathrm{div}\!\Bigl(p_t u_t^{\text{target}}+\frac{\sigma_t^2}{2}p_t\nabla\log p_t\Bigr)(x)+\frac{\sigma_t^2}{2}\Delta p_t(x) \\ &=\ -\,\mathrm{div}\!\left(p_t\Bigl[u_t^{\text{target}}+\frac{\sigma_t^2}{2}\nabla\log p_t\Bigr]\right)(x)+\frac{\sigma_t^2}{2}\Delta p_t(x), \end{aligned} $$其中 $(i)$ 用连续性方程,$(iii)$ 使用 $\Delta w=\mathrm{div}(\nabla w)$,$(iv)$ 用 $\nabla\log p_t=\nabla p_t/p_t$ 与散度线性性。故式 (25) 满足 FPE,从而 $X_t\sim p_t$,证毕。
备注 16(Remark 16:Langevin dynamics,朗之万动力学)
当概率路径为静态 $p_t=p$(固定分布)时,令 $u_t^{\text{target}}=0$,得到
$$\mathrm{d}X_t=\frac{\sigma_t^2}{2}\nabla\log p(X_t)\,\mathrm{d}t+\sigma_t\,\mathrm{d}W_t, \quad (31)$$这就是著名的朗之万动力学(Langevin dynamics,LD)。因为 $p_t$ 静止,$\partial_t p_t(x)=0$,由定理 13 知 $p$ 是 LD 的不变分布:
$$X_0\sim p\ \Longrightarrow\ X_t\sim p\quad (t\ge 0).$$在温和条件下,如果 $X_0\sim p'\ne p$,则 $X_t\Rightarrow p$。因此 LD 被广泛用于分子动力学(molecular dynamics)、MCMC 及贝叶斯统计与自然科学中的许多计算任务。
总结 17(Summary 17:Derivation of the Training Target,训练目标的推导)
流的训练目标是边缘向量场 $u_t^{\text{target}}$。构造流程如下:
选择满足 $p_0(\cdot|z)=p_{\text{init}},\ p_1(\cdot|z)=\delta_z$ 的条件概率路径 $p_t(x|z)$。
找到一个条件向量场 $u_t^{\text{flow}}(x|z)$(或其对应流 $\psi_t^{\text{target}}(x|z)$),使得
$$ X*0\sim p*{\text{init}}\ \Longrightarrow\ X_t=\psi_t^{\text{target}}(X_0\mid z)\sim p_t(\cdot\mid z), $$或等价地,$u_t^{\text{target}}(\cdot|z)$ 满足连续性方程。
定义边缘向量场
$$ u*t^{\text{target}}(x)=\int u_t^{\text{target}}(x\mid z)\, \frac{p_t(x\mid z)\,p*{\text{data}}(z)}{p_t(x)}\,\mathrm{d}z. \quad (32) $$则该 ODE 的边缘路径为
$$ X*0\sim p*{\text{init}},\qquad \mathrm{d}X_t=u_t^{\text{target}}(X_t)\,\mathrm{d}t \ \Longrightarrow\ X_t\sim p_t,\quad (0\le t\le 1). \quad (33) $$特别地,$X_1\sim p_{\text{data}}$,因此 $u_t^{\text{target}}$ “把噪声转为数据”。
扩展到 SDE. 对任意随时间变化的扩散系数 $\sigma_t\ge 0$,可将 ODE 扩展为具有同一边缘概率路径的 SDE:
$$ X*0\sim p*{\text{init}},\quad \mathrm{d}X_t=\Bigl[u_t^{\text{target}}(X_t)+\frac{\sigma_t^2}{2}\nabla\log p_t(X_t)\Bigr]\mathrm{d}t+\sigma_t\,\mathrm{d}W_t \quad (34) $$$$\Longrightarrow\ X_t\sim p_t,\quad (0\le t\le 1). \quad (35)$$其中 $\nabla\log p_t(x)$ 为边缘得分函数,可由条件得分函数表示为
$$ \nabla\log p*t(x)=\int \nabla\log p_t(x\mid z)\, \frac{p_t(x\mid z)\,p*{\text{data}}(z)}{p_t(x)}\,\mathrm{d}z. \quad (36) $$特别地,对于上述 SDE 的轨迹 $X_t$,有 $X_1\sim p_{\text{data}}$,因此该 SDE 如期地“把噪声转换成数据”。一个重要的例子是高斯概率路径(Gaussian Probability Path),它给出以下公式:
$$p_t(x\mid z)=\mathcal{N}\!\left(x;\ \alpha_t z,\ \beta_t^2 I_d\right), \quad (37)$$$$ u_t^{\text{flow}}(x\mid z)=\Bigl(\dot{\alpha}\_t-\tfrac{\dot{\beta}\_t}{\beta_t}\alpha_t\Bigr)z \;+\;\tfrac{\dot{\beta}\_t}{\beta_t}\,x, \quad (38) $$$$\nabla\log p_t(x\mid z)= -\,\frac{x-\alpha_t z}{\beta_t^2}, \quad (39)$$其中 $\alpha_t,\beta_t\in\mathbb{R}$ 是噪声调度器(Noise Schedulers):它们是关于时间的连续可微、单调函数,并满足边界条件 $\alpha_0=\beta_1=0,\ \alpha_1=\beta_0=1$。
4 训练生成模型(Training the Generative Model)#
在前两节中,我们构造了一个由神经网络给出的向量场 $u_t^\theta$ 的生成模型,并推导了训练目标 $u_t^{\text{target}}$ 的形式。本节讨论如何训练神经网络 $u_t^\theta$ 去逼近该目标。我们先在常微分方程(ODE)框架中给出流匹配(Flow Matching,FM),随后扩展到随机微分方程(SDE),得到得分匹配(Score Matching,SM)。特别地,在高斯概率路径(Gaussian probability paths)情形下可以恢复到去噪扩散模型(Denoising Diffusion Models)。到本节结束,我们会得到一个使用 ODE/SDE 端到端训练与采样的完整流程。
4.1 流匹配(Flow Matching,FM)#
像之前一样,考虑如下流模型(flow model):
$$ X_0 \sim p_{\text{init}},\quad \mathrm{d}X_t = u_t^\theta(X_t)\,\mathrm{d}t. \quad (40) $$我们的目标是让神经网络 $u_t^\theta$ 等于边缘目标向量场 $u_t^{\text{target}}$。换句话说,希望找到参数 $\theta$ 使得 $u_t^\theta \approx u_t^{\text{target}}$。下面约定:$\mathrm{Unif}=\mathrm{Unif}_{[0,1]}$ 表示区间 $[0,1]$ 上的均匀分布(Uniform distribution,Unif),$\mathbb{E}$ 表示期望(Expectation,E)。
一个直观的办法是采用均方误差(Mean Squared Error,MSE)回归得到流匹配损失(Flow Matching loss):
$$ \mathcal{L}_{\text{FM}}(\theta) = \mathbb{E}_{\,t\sim\mathrm{Unif},\,x\sim p_t}\!\left[\left\|u_t^\theta(x)-u_t^{\text{target}}(x)\right\|^2\right] \quad (41) $$并利用条件采样写成等价形式
$$ \overset{(i)}{=}\; \mathbb{E}_{\,t\sim\mathrm{Unif},\,z\sim p_{\text{data}},\,x\sim p_t(\cdot\mid z)} \!\left[\left\|u_t^\theta(x)-u_t^{\text{target}}(x)\right\|^2\right]. \quad (42) $$其中 $p_t(x)=\int p_t(x\mid z)\,p_{\text{data}}(z)\,\mathrm{d}z$ 是边缘概率路径(marginal probability path),而 $(i)$ 使用的是式 (13) 给出的采样过程。直观地说,该损失执行以下步骤:首先从 $t\in[0,1]$ 均匀采样一个时间;其次从数据集中采样 $z$,再从条件分布 $p_t(\cdot\mid z)$ 采样 $x$(比如向 $z$ 加一点噪声);接着计算网络 $u_t^\theta(x)$ 的输出;最后把该输出与边缘目标向量场 $u_t^{\text{target}}(x)$ 做均方误差。
尽管我们已通过定理 10 知道 $u_t^{\text{target}}$ 的表达式
$$ u_t^{\text{target}}(x) =\int u_t^{\text{target}}(x\mid z)\,\frac{p_t(x\mid z)\,p_{\text{data}}(z)}{p_t(x)}\,\mathrm{d}z, \quad (43) $$但由于上式包含难以计算的积分,直接使用并不高效。相反,我们将利用这样一个事实:条件速度场(conditional velocity field)$u_t^{\text{target}}(x\mid z)$ 是可计算(tractable)的。由此定义条件流匹配损失(Conditional Flow Matching,CFM):
$$ \mathcal{L}_{\text{CFM}}(\theta) =\mathbb{E}_{\,t\sim\mathrm{Unif},\,z\sim p_{\text{data}},\,x\sim p_t(\cdot\mid z)} \!\left[\left\|u_t^\theta(x)-u_t^{\text{target}}(x\mid z)\right\|^2\right]. \quad (44) $$与式 (41) 相比,这里用的是条件向量场 $u_t^{\text{target}}(x\mid z)$ 而非边缘向量场 $u_t^{\text{target}}(x)$。由于我们拥有 $u_t^{\text{target}}(x\mid z)$ 的解析公式,上述损失易于最小化。也许你会问:既然我们真正关心的是边缘向量场,为什么要回归条件向量场?事实是:显式地回归这个可计算的条件向量场,隐式地就回归了那个不可直接计算的边缘向量场。
定理 18(Theorem 18)
边缘流匹配损失与条件流匹配损失只差一个与 $\theta$ 无关的常数:
$$\mathcal{L}_{\text{FM}}(\theta) = \mathcal{L}_{\text{CFM}}(\theta) + C.$$因而它们的梯度相同,$\nabla_\theta \mathcal{L}_{\text{FM}}(\theta)=\nabla_\theta \mathcal{L}_{\text{CFM}}(\theta)$。 使用随机梯度下降最小化 $\mathcal{L}_{\text{CFM}}$ 与最小化 $\mathcal{L}_{\text{FM}}$ 等价;当模型足够表达时,最优解满足 $u_t^{\theta^\star}=u_t^{\text{target}}$。
证明(Proof)。我们通过将均方误差(mean-squared error, MSE)展开为三项并去除与参数无关的常数来完成证明:
$$ \begin{aligned}\mathcal{L}_{\mathrm{FM}}(\theta)&\stackrel{(i)}{=} \mathbb{E}_{t\sim \mathrm{Unif},\, x\sim p_t}\!\left[\left\|u_t^\theta(x)-u_t^{\text{target}}(x)\right\|^2\right] \\&\stackrel{(ii)}{=} \mathbb{E}_{t\sim \mathrm{Unif},\, x\sim p_t}\!\left[\|u_t^\theta(x)\|^2-2\,u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x)+\|u_t^{\text{target}}(x)\|^2\right] \\&\stackrel{(iii)}{=} \mathbb{E}_{t\sim \mathrm{Unif},\, x\sim p_t}\!\left[\|u_t^\theta(x)\|^2\right] -2\,\mathbb{E}_{t\sim \mathrm{Unif},\, x\sim p_t}\!\left[u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x)\right] +\underbrace{\mathbb{E}_{t\sim \mathrm{Unif}_{[0,1]},\, x\sim p_t}\!\left[\|u_t^{\text{target}}(x)\|^2\right]}_{=:C_1} \\&\stackrel{(iv)}{=} \mathbb{E}_{\substack{t\sim \mathrm{Unif},\, z\sim p_{\text{data}}\, x\sim p_t(\cdot|z)}}\!\left[\|u_t^\theta(x)\|^2\right] -2\,\mathbb{E}_{\substack{t\sim \mathrm{Unif},\, x\sim p_t}}\!\left[u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x)\right] + C_1 .\end{aligned} $$其中:(i) 由定义得到;(ii) 用到公式 $\|a-b\|^2=\|a\|^2-2a^\top b+\|b\|^2$;(iii) 定义常数 $C_1$;(iv) 使用式 (13) 给出的对 $p_t$ 的采样过程。
现在重写第二项:
$$ \begin{aligned} \mathbb{E}_{t\sim\mathrm{Unif},\,x\sim p_t}\!\left[u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x)\right] &\stackrel{(i)}{=} \int_0^1 \!\!\int p_t(x)\, u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x)\, \mathrm{d}x\, \mathrm{d}t \\ &\stackrel{(ii)}{=} \int_0^1 \!\!\int p_t(x)\, u_t^\theta(x)^{\!\top} \Bigg[\int u_t^{\text{target}}(x|z)\, \frac{p_t(x|z)\, p_{\text{data}}(z)}{p_t(x)}\, \mathrm{d}z\Bigg] \mathrm{d}x\, \mathrm{d}t \\ &\stackrel{(iii)}{=} \int_0^1 \!\!\iint u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x|z)\, p_t(x|z)\, p_{\text{data}}(z)\, \mathrm{d}z\, \mathrm{d}x\, \mathrm{d}t \\ &\stackrel{(iv)}{=} \mathbb{E}_{\substack{t\sim \mathrm{Unif},\, z\sim p_{\text{data}}\, x\sim p_t(\cdot|z)}}\!\left[u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x|z)\right]. \end{aligned} $$(i) 把期望写成积分;(ii) 用到式 (43);(iii) 利用积分的线性性;(iv) 再把积分写回期望。注意这是关键一步:起初使用的是边缘向量场(marginal vector field)$u_t^{\text{target}}(x)$,最后得到的是条件向量场(conditional vector field)$u_t^{\text{target}}(x|z)$。
把上式代回 $\mathcal{L}_{\mathrm{FM}}$ 可得:
$$ \begin{aligned} \mathcal{L}_{\mathrm{FM}}(\theta)&\stackrel{(i)}{=} \mathbb{E}_{\substack{t\sim\mathrm{Unif},\, z\sim p_{\text{data}}\, x\sim p_t(\cdot|z)}}\!\left[\|u_t^\theta(x)\|^2\right]-2\,\mathbb{E}_{\substack{t\sim\mathrm{Unif},\, z\sim p_{\text{data}}, x\sim p_t(\cdot|z)}}\!\left[u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x|z)\right]+ C_1 \\&\stackrel{(ii)}{=} \mathbb{E}_{\substack{t\sim\mathrm{Unif},\, z\sim p_{\text{data}}\, x\sim p_t(\cdot|z)}}\!\left[\|u_t^\theta(x)\|^2 -2\,u_t^\theta(x)^{\!\top} u_t^{\text{target}}(x|z) + \|u_t^{\text{target}}(x|z)\|^2 - \|u_t^{\text{target}}(x|z)\|^2\right] + C_1 \\&\stackrel{(iii)}{=} \mathbb{E}_{\substack{t\sim\mathrm{Unif},\, z\sim p_{\text{data}}\, x\sim p_t(\cdot|z)}}\!\left[\|u_t^\theta(x)-u_t^{\text{target}}(x|z)\|^2\right] + \underbrace{\mathbb{E}_{\substack{t\sim\mathrm{Unif},\, z\sim p_{\text{data}}\, x\sim p_t(\cdot|z)}}\!\left[- \|u_t^{\text{target}}(x|z)\|^2\right]}_{C_2} + C_1 \\&\stackrel{(iv)}{=} \mathcal{L}_{\mathrm{CFM}}(\theta) + \underbrace{C_2 + C_1}_{=:C} , \end{aligned} $$其中 (i) 代入上述结果,(ii) 加上并减去相同的一项,(iii) 再次使用 $\|a-b\|^2=\|a\|^2-2a^\top b+\|b\|^2$,(iv) 把与 $\theta$ 无关的项并入常数 $C_2$。至此证明完成。
一旦训练好 $u_t^\theta$,即可模拟流模型(flow model)以生成样本:
$$ \mathrm{d}X_t = u_t^\theta(X_t)\,\mathrm{d}t,\quad X_0\sim p_{\text{init}} \quad (45) $$例如用算法 1 进行数值积分,从而得到 $X_1\sim p_{\text{data}}$。整个流程在文献中被称为流匹配(Flow Matching, FM)。下面给出在高斯条件概率路径下的条件流匹配(Conditional Flow Matching, CFM)损失。
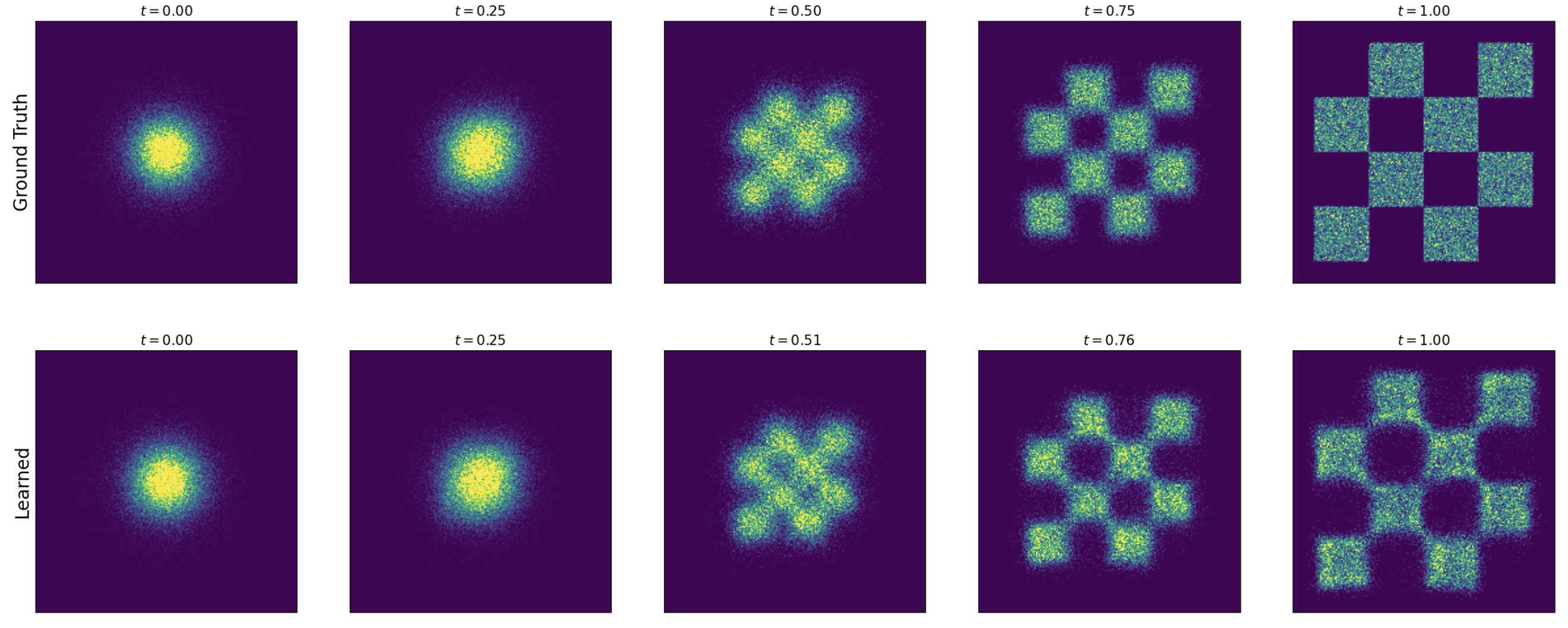
图 9:定理 18 的示意图,采用高斯 CondOT 概率路径:从一个训练好的流匹配模型中模拟 ODE。数据分布为棋盘格模式(右上角)。上排:来自真实边缘概率路径 $p_t(x)$ 的直方图。下排:来自流匹配模型样本的直方图。可以看到,训练后上下两排相互吻合(在训练误差范围内)。该模型是使用算法 5 进行训练的。
示例 19(高斯条件概率路径的流匹配) 回到高斯条件概率路径 $p_t(\cdot|z)=\mathcal{N}(\alpha_t z,\beta_t^2 I_d)$。从该路径采样的方法为
$$\varepsilon\sim\mathcal{N}(0,I_d)\ \Rightarrow\ x_t=\alpha_t z+\beta_t\varepsilon\sim \mathcal{N}(\alpha_t z,\beta_t^2 I_d)=p_t(\cdot|z). \quad (46)$$由式 (21) 可得条件向量场
$$u_t^{\text{target}}(x|z)=\left(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\right)z+\frac{\dot{\beta}_t}{\beta_t}x, \quad (47)$$其中 $\dot{\alpha}_t=\partial_t\alpha_t,\ \dot{\beta}_t=\partial_t\beta_t$ 为时间导数。代入得 CFM 损失
$$\begin{aligned}\mathcal{L}_{\mathrm{CFM}}(\theta)&= \mathbb{E}_{\substack{t\sim\mathrm{Unif},\, z\sim p_{\text{data}}\, x\sim \mathcal{N}(\alpha_t z,\beta_t^2 I_d)}}\!\left[\left\|u_t^\theta(x)-\big(\dot{\alpha}_t-\tfrac{\dot{\beta}_t}{\beta_t}\alpha_t\big)z+\tfrac{\dot{\beta}_t}{\beta_t}x\right\|^2\right] \\&\stackrel{(i)}{=} \mathbb{E}_{t\sim\mathrm{Unif},\, z\sim p_{\text{data}},\, \varepsilon\sim\mathcal{N}(0,I_d)}\!\left[\left\|u_t^\theta(\alpha_t z+\beta_t\varepsilon)-\big(\dot{\alpha}_t z+\dot{\beta}_t\varepsilon\big)\right\|^2\right],\end{aligned}$$其中 (i) 用式 (46) 把 $x$ 替换为 $\alpha_t z+\beta_t\varepsilon$。这一形式非常简洁:采样 $z$ 与噪声 $\varepsilon$,随后计算 MSE。 取特例 $\alpha_t=t,\ \beta_t=1-t$,得到常称为(高斯)CondOT(Conditional Optimal Transport,条件最优传输)概率路径的 $p_t(x|z)=\mathcal{N}(t z,(1-t)^2)$。此时 $\dot{\alpha}_t=1,\ \dot{\beta}_t=-1$,于是
$$\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},\, z\sim p_{\text{data}},\, \varepsilon\sim\mathcal{N}(0,I_d)}\left[\left\|u_t^\theta\!\big(tz+(1-t)\varepsilon\big)-(z-\varepsilon)\right\|^2\right].$$许多 SOTA 模型(如 Stable Diffusion 3、Meta 的 Movie Gen Video 等)都采用了这一简单而有效的训练过程。
输入:数据集 $z\sim p_{\text{data}}$,神经网络 $u_t^\theta$
对每个 mini-batch 执行:
- 从数据集中采样 $z$;
- 采样 $t\sim\mathrm{Unif}_{[0,1]}$;
- 采样噪声 $\varepsilon\sim\mathcal{N}(0,I_d)$;
- 设 $x=t z+(1-t)\varepsilon$(一般情形:$x\sim p_t(\cdot|z)$);
- 计算损失:
- 通过对 $\mathcal{L}(\theta)$ 的梯度下降更新参数 $\theta$;
4.2 得分匹配(Score Matching,SM)#
让我们把先前从 ODEs 推导出的算法扩展到 SDEs。记住:我们可以把目标 ODE 扩展为具有相同边缘分布的 SDE:
$$ \mathrm{d}X_t \;=\; \Big[\,u^{\text{target}}_{t}(X_t)\;+\;\tfrac{\sigma_t^2}{2}\,\nabla \log p_t(X_t)\,\Big]\mathrm{d}t\;+\;\sigma_t\,\mathrm{d}W_t \quad (48) $$$$ X_0 \sim p_{\text{init}} \quad (49) $$$$ \Rightarrow \quad X_t \sim p_t \quad (0 \le t \le 1) \quad (50) $$其中,$u^{\text{target}}_{t}$ 是边缘向量场(marginal vector field),$\nabla\log p_t(x)$ 是边缘得分函数(marginal score function),且可由下面的公式表示:
$$ \nabla \log p_t(x) \;=\; \int \nabla \log p_t(x\mid z)\,\frac{p_t(x\mid z)\,p_{\text{data}}(z)}{p_t(x)}\,\mathrm{d}z. \quad (51) $$为了近似边缘得分 $\nabla\log p_t$,我们使用一个称为得分网络(score network,记作 $s_t^\theta:\mathbb{R}^d\times[0,1]\rightarrow\mathbb{R}^d$)的神经网络。与之前相同,我们可以设计得分匹配损失(Score Matching,SM)和条件得分匹配损失(Conditional Score Matching,CSM):
- 得分匹配损失(使用边缘得分 $\nabla\log p_t$): $$ \mathcal{L}_{\text{SM}}(\theta) \;=\; \mathbb{E}_{\,t\sim\mathrm{Unif},\,z\sim p_{\text{data}},\,x\sim p_t(\cdot\mid z)} \big[\ \|\,s_t^\theta(x)\;-\;\nabla\log p_t(x)\,\|^2\ \big]. $$
- 条件得分匹配损失(使用条件得分 $\nabla\log p_t(x\mid z)$): $$ \mathcal{L}_{\text{CSM}}(\theta) \;=\; \mathbb{E}_{\,t\sim\mathrm{Unif},\,z\sim p_{\text{data}},\,x\sim p_t(\cdot\mid z)} \big[\ \|\,s_t^\theta(x)\;-\;\nabla\log p_t(x\mid z)\,\|^2\ \big]. $$
如同之前一样,我们理想地希望最小化得分匹配损失,但我们并不知道 $\nabla\log p_t(x)$。好在条件得分匹配损失是一个可处理的替代项:
定理 20
得分匹配损失与条件得分匹配损失相差一个常数:
$$\mathcal{L}_{\text{SM}}(\theta) \;=\; \mathcal{L}_{\text{CSM}}(\theta) + C,$$其中 $C$ 与参数 $\theta$ 无关。因此,它们的梯度一致:
$$\nabla_\theta \mathcal{L}_{\text{SM}}(\theta) \;=\; \nabla_\theta \mathcal{L}_{\text{CSM}}(\theta).$$特别地,在极小化器 $\theta^\star$ 处,有
$$s_t^{\theta^\star} \;=\; \nabla\log p_t.$$
证明思路:注意式(51)与(43)形式相同,因此证明与定理 18 的证明完全一致,只需将 $u^{\text{target}}_{t}$ 替换为 $\nabla\log p_t$。
上述过程刻画了训练扩散模型(diffusion model)的基础做法。训练后,我们可以任选扩散系数 $\sigma_t\ge 0$,并模拟下式 SDE 以生成样本:
$$ X_0 \sim p_{\text{init}},\quad \mathrm{d}X_t \;=\; \Big[\,u_t^\theta(X_t)\;+\;\tfrac{\sigma_t^2}{2}\,s_t^\theta(X_t)\,\Big]\mathrm{d}t\;+\;\sigma_t\,\mathrm{d}W_t. \quad (52) $$在理想情形下,每个 $\sigma_t$ 都会在完美训练时给出 $X_1\sim p_{\text{data}}$。实际中会有两类误差:(1)SDE 数值模拟误差;(2)训练误差(即 $s_t^\theta$ 并不完全等于 $\nabla\log p_t$)。因此存在一个未知的最优噪声水平 $\sigma_t$,一般通过经验测试不同取值来确定。乍看之下,我们似乎需要同时学习 $s_t^\theta$ 和 $u_t^\theta$ 才能使用扩散模型,相比流模型(flow model)要多一个输出。但对于高斯概率路径(Gaussian probability path),$s_t^\theta$ 与 $u_t^\theta$ 可以互相转换,因此无需分别训练。
备注 21(Remark 21:去噪扩散模型,Denoising Diffusion Models,DDM)
如果你熟悉扩散模型,你很可能听过“去噪扩散模型”。该模型非常流行,以至于大家常常直接称为“扩散模型”。在本文语境下,它们就是以高斯形式的概率路径 $p_t(\cdot\mid z)=\mathcal{N}(\alpha_t z,\,\beta_t^2 I_d)$ 的模型。不过需注意,最早的一些扩散模型论文采用了与此不同的时间约定(time convention,时间被反向),因此需要做时间重标度,并使用所谓的前向过程(forward processes;见第 4.3 节)来构造轨迹。
例 22(去噪扩散模型:高斯概率路径上的得分匹配,Denoising Diffusion Models: Score Matching for Gaussian Probability Paths)
对 $p_t(x\mid z)=\mathcal{N}(\alpha_t z,\,\beta_t^2 I_d)$,条件得分为
$$\nabla\log p_t(x\mid z) \;=\; -\,\frac{x-\alpha_t z}{\beta_t^2}. \quad (53)$$代入条件得分匹配损失可得
$$ \begin{aligned} \mathcal{L}_{\mathrm{CSM}}(\theta) &=\mathbb{E}_{\,t\sim\mathrm{Unif},\, z\sim p*{\text{data}},\, x\sim p_t(\cdot\mid z)} \Big[\ \big\|\, s_t^\theta(x)\;+\;\tfrac{x-\alpha_t z}{\beta_t^2}\,\big\|^2\ \Big] \\ &\overset{(i)}{=}\mathbb{E}*{\,t\sim\mathrm{Unif},\, z\sim p*{\text{data}},\, \varepsilon\sim\mathcal{N}(0,I_d)} \Big[\ \big\|\, s_t^\theta(\alpha_t z+\beta_t\varepsilon)\;+\;\tfrac{\varepsilon}{\beta_t}\,\big\|^2\ \Big] \\ &=\mathbb{E}*{\,t\sim\mathrm{Unif},\, z\sim p\_{\text{data}},\, \varepsilon\sim\mathcal{N}(0,I_d)} \Big[\ \tfrac{1}{\beta_t^2}\,\big\|\, \beta_t\, s_t^\theta(\alpha_t z+\beta_t\varepsilon)\;+\;\varepsilon \big\|^2\ \Big]. \end{aligned} $$其中 $(i)$ 处用到了 $x=\alpha_t z+\beta_t\varepsilon$。注意到 $s_t^\theta$ 实质上在学习用于把数据样本 $z$ 污染为 $x$ 的噪声。因此,该训练损失又称去噪得分匹配(denoising score matching)。但当 $\beta_t\to 0$ 时,上式会出现数值不稳定(即仅用得分匹配在实践中常需加足够噪声)。最早的一些工作(见去噪扩散概率模型(Denoising Diffusion Probabilistic Models,DDPM))提出:去掉损失里的常数因子 $1/\beta_t^2$,并把得分网络重参数化为噪声预测网络(noise predictor network)$\varepsilon_t^\theta:\mathbb{R}^d\times[0,1]\to\mathbb{R}^d$:
$$-\beta_t\,s_t^\theta(x) \;=\; \varepsilon_t^\theta(x).$$于是得到 DDPM 的训练目标
$$\mathcal{L}_{\mathrm{DDPM}}(\theta)=\mathbb{E}_{\,t\sim\mathrm{Unif},\; z\sim p_{\text{data}},\; \varepsilon\sim\mathcal{N}(0,I_d)}\Big[\,\big\|\,\varepsilon_t^\theta(\alpha_t z+\beta_t\varepsilon)\;-\;\varepsilon\,\big\|^2\,\Big].$$如前所述,网络 ( $\varepsilon_t^\theta$ ) 本质上是在学习预测用来对数据样本 ( $z$ ) 加噪的那段噪声。我们在算法 4 中总结了训练流程。
输入:数据集样本 $z\sim p_{\text{data}}$;得分网络 $s_t^\theta$ 或噪声预测器 $\varepsilon_t^\theta$
对每个 mini-batch 执行:
- 从数据集中采样 $z$;
- 采样随机时间 $t\sim\mathrm{Unif}_{[0,1]}$;
- 采样噪声 $\varepsilon\sim\mathcal{N}(0,I_d)$;
- 设 $x_t=\alpha_t z+\beta_t\varepsilon$(一般情形:$x_t\sim p_t(\cdot|z)$);
- 计算损失:
一般情形:$\mathcal{L}(\theta)=\big\|\, s_t^\theta(x_t)\;-\;\nabla_{x_t}\log p_t(x_t\mid z)\,\big\|^2$
- 用梯度下降更新 $\theta$。
“除了其简单性之外,高斯概率路径还有一个有用的性质:只要学会 $s_t^{\theta}$ 或 $\varepsilon_t^{\theta}$,就等于自动学会了 $u_t^{\theta}$;反之亦然:”
命题 1(高斯概率路径的转换公式,Conversion formula for Gaussian probability path)
对于 $p_t(x\mid z)=\mathcal{N}(\alpha_t z,\beta_t^2 I_d)$,条件向量场与条件得分满足
$$u_t^{\text{target}}(x\mid z)\;=\;\Big(\beta_t^2\,\tfrac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\,\beta_t\Big)\,\nabla\log p_t(x\mid z)\;+\;\tfrac{\dot\alpha_t}{\alpha_t}\,x,$$进而边缘向量场与边缘得分满足
$$u_t^{\text{target}}(x)\;=\;\Big(\beta_t^2\,\tfrac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\,\beta_t\Big)\,\nabla\log p_t(x)\;+\;\tfrac{\dot\alpha_t}{\alpha_t}\,x.$$其中关于边缘向量场的上式在文献中被称为概率流 ODE(Probability Flow ODE;更严格地说,是对应的 ODE)。
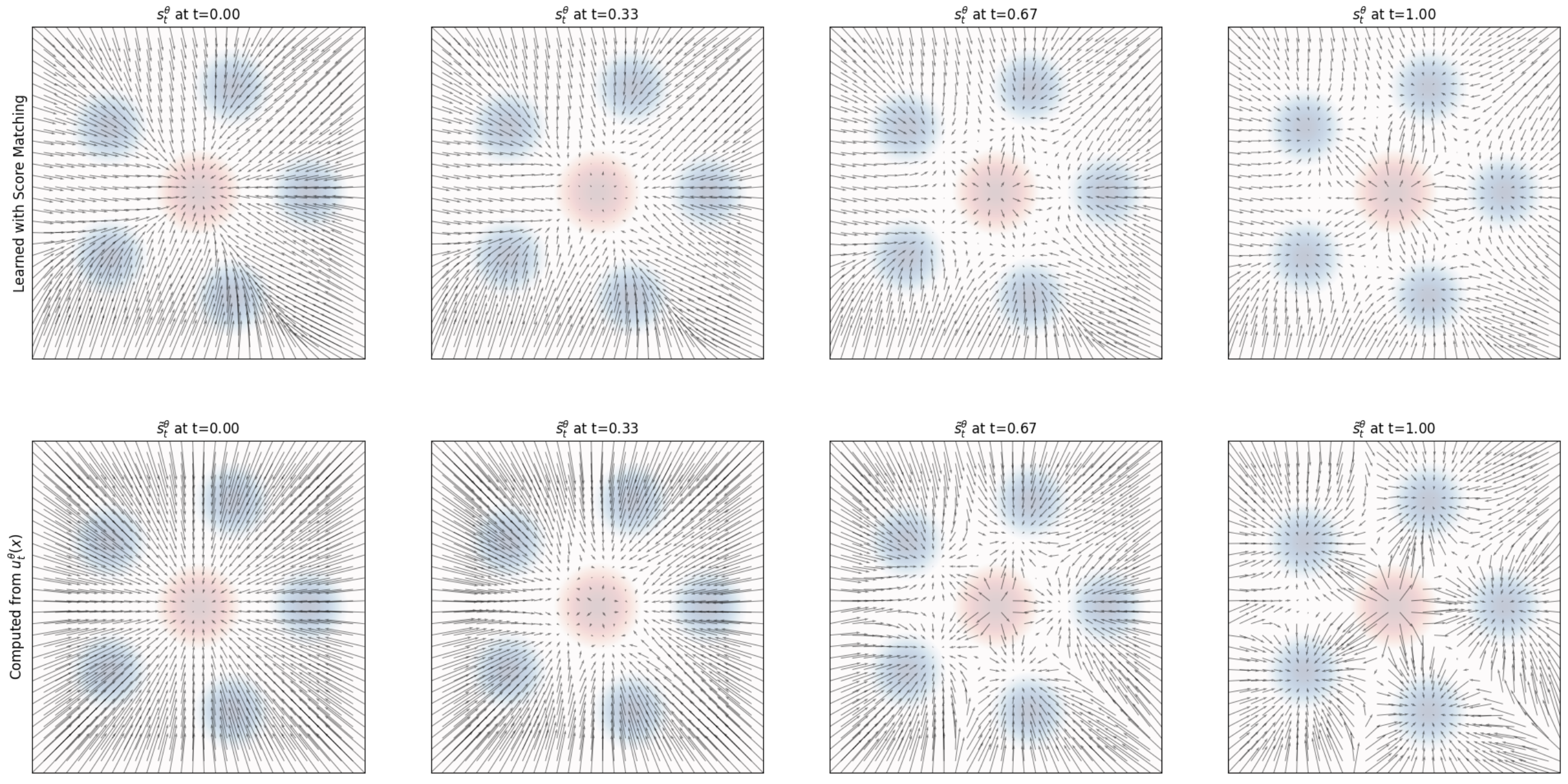
图 10:以两种不同方式得到的 score 的比较。上图:通过 score matching 独立学习得到的得分场 $s_t^\theta(x)$ 的可视化(见算法 4)。下图:使用式 (55) 中的 $u_t^\theta(x)$ 进行参数化所得到的得分场 $\tilde{s}_t^\theta(x)$ 的可视化。
证明(Proof) 对于条件向量场(conditional vector field)与条件得分(conditional score),可推出
$$ u_t^{\text{target}}(x\!\mid\! z)=\Big(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\Big)z+\frac{\dot{\beta}_t}{\beta_t}\,x\overset{(i)}{=}\Big(\beta_t^2\frac{\dot{\alpha}_t}{\alpha_t}-\dot{\beta}_t\beta_t\Big)\Big(\frac{\alpha_t z-x}{\beta_t^2}\Big)+\frac{\dot{\alpha}_t}{\alpha_t}x=\Big(\beta_t^2\frac{\dot{\alpha}_t}{\alpha_t}-\dot{\beta}_t\beta_t\Big)\nabla\log p_t(x\!\mid\! z)+\frac{\dot{\alpha}_t}{\alpha_t}x . $$其中 $(i)$ 仅为代数化简。对 $z$ 积分后,同样的恒等式对边缘流向量场(marginal flow vector field)与边缘得分函数(marginal score function)成立:
$$ \begin{aligned}u_t^{\text{target}}(x)&=\int u_t^{\text{target}}(x\!\mid\! z)\, \frac{p_t(x\!\mid\! z)\,p_{\text{data}}(z)}{p_t(x)}\,dz \\&=\int\Big[\Big(\beta_t^2\frac{\dot{\alpha}_t}{\alpha_t}-\dot{\beta}_t\beta_t\Big)\nabla\log p_t(x\!\mid\! z)+\frac{\dot{\alpha}_t}{\alpha_t}x\Big]\,\frac{p_t(x\!\mid\! z)\,p_{\text{data}}(z)}{p_t(x)}\,dz \\&\overset{(i)}{=}\Big(\beta_t^2\frac{\dot{\alpha}_t}{\alpha_t}-\dot{\beta}_t\beta_t\Big)\nabla\log p_t(x)+\frac{\dot{\alpha}_t}{\alpha_t}x .\end{aligned} $$其中 $(i)$我们使用了式(51)。
我们可以利用“转换公式(conversion formula)”在得分网络(score network)$s_t^\theta$ 与向量场网络(vector field network)$u_t^\theta$ 之间相互参数化:
$$ u_t^\theta(x)=\Big(\beta_t^2\frac{\dot{\alpha}_t}{\alpha_t}-\dot{\beta}_t\beta_t\Big)s_t^\theta(x) +\frac{\dot{\alpha}_t}{\alpha_t}\,x .\quad (54) $$类似地,只要 $\,\beta_t^2\dot{\alpha}_t-\alpha_t\dot{\beta}_t\beta_t\neq 0\,$(对 $t\in[0,1)$ 总成立),就有
$$ s_t^\theta(x)=\frac{\alpha_t u_t^\theta(x)-\dot{\alpha}_t x}{\beta_t^2\dot{\alpha}_t-\alpha_t\dot{\beta}_t\beta_t}\,.\quad (55) $$基于上述参数化,可以证明:去噪得分匹配(denoising score matching,DSM)与条件流匹配(conditional flow matching,CFM)的损失函数仅相差一个常数。于是,对于高斯概率路径(Gaussian probability paths,GPPs),无需分别训练边缘得分与边缘向量场——知道其中之一即可计算出另一个。换言之,我们可以任选用流匹配或得分匹配来训练。图 10 中比较了用得分匹配得到的得分与由式 (55) 参数化得到的得分。若我们已训练好得分网络 $s_t^\theta$,由式 (52) 可知,可在任意 $\sigma_t\ge 0$ 下从如下 SDE 进行采样:
$$ X_0\sim p_{\text{init}},\quad dX_t=\Big[\Big(\beta_t^2\frac{\dot{\alpha}_t}{\alpha_t}-\dot{\beta}_t\beta_t+\frac{\sigma_t^2}{2}\Big)s_t^\theta(x)+\frac{\dot{\alpha}_t}{\alpha_t}x\Big]dt+\sigma_t\,dW_t.\quad (56) $$从而(忽略训练与数值模拟误差)获得 $X_1\sim p_{\text{data}}$。这对应于从去噪扩散模型(denoising diffusion model,DDM)进行随机采样(stochastic sampling)。
4.3 扩散模型(Diffusion Models,DMs)文献导读#
在文献中,围绕扩散模型(Diffusion Models,DMs)与流匹配(Flow Matching,FM)形成了一个模型家族。阅读这些论文时,你常会发现对同一类材料存在不同(但等价)的表述方式,这有时会让人困惑。为此,我们简要概览这些框架及其差异,并将它们置于历史语境中。理解本节并非掌握本文其余部分的必要条件,但当你阅读原始文献时,它可以作为参考。
离散时间 vs. 连续时间#
最早的去噪扩散模型论文 5 6 7 并未使用随机微分方程(Stochastic Differential Equations,SDEs),而是在离散时间下构造马尔可夫链(Markov chains),即采用时间步 $t=0,1,2,3,\ldots$。至今仍有大量工作沿用这种离散时间表述。该构造因其简单而颇具吸引力,但其缺点在于:它迫使你在训练前就选择时间离散化方案。另外,损失函数需要通过证据下界(Evidence Lower Bound,ELBO)来近似——顾名思义,它只是我们真正希望最小化的损失的下界。后来,Song 等人 8 证明这些构造本质上是对连续时间 SDE 的一种近似。此外,在连续时间情形下,ELBO 损失是“收紧”的(即不再是下界);例如,本书中的定理 18 和定理 20 给出的都是等式而非下界——而在离散时间情形中则不同。由于被认为在数学上更“干净”,且训练后可通过 ODE/SDE 采样器(ODE/SDE samplers)来控制仿真误差,SDE 构造因此流行起来。但需强调,两类模型采用的是同一个损失,并无本质差别。
“前向过程(Forward Process)” vs. 概率路径(Probability Path)#
第一波去噪扩散模型 5 6 7 8 并未使用“概率路径(Probability Path)”这一术语,而是对数据点 $z\in\mathbb{R}^d$ 构造一个所谓的前向过程(forward process)。其形式为如下 SDE:
$$ \bar{X}_0 = z,\quad \mathrm{d}\bar{X}_t = u_t^{\mathrm{forw}}\big(\bar{X}_t\big)\,\mathrm{d}t + \sigma_t^{\mathrm{forw}}\, \mathrm{d}\bar{W}_t \quad (57) $$其思想是:先从数据分布抽样 $z\sim p_{\text{data}}$,再模拟该前向过程,从而“腐化/加噪”数据。该前向过程被设计为当 $t\to\infty$ 时,其分布收敛到高斯分布 $\mathcal{N}(0,I_d)$。换言之,对于足够大的 $T>0$,有近似关系 $ \bar{X}_T \sim \mathcal{N}(0,I_d) $。 注意,这实质上对应于一个概率路径:在 $\bar{X}_0=z$ 条件下,$\bar{X}_t$ 的条件分布是一个条件概率路径 $\bar{p}_t(z)$;而将 $z\sim p_{\text{data}}$ 积分边缘化后得到的 $\bar{X}_t$ 分布,对应于一个边缘概率路径 $\bar{p}_t$。然而采用这种构造时,我们需要已知 $\bar{X}_t\mid \bar{X}_0=z$ 的闭式分布,才能在训练中避免显式模拟 SDE。这本质上将向量场 $u_t^{\mathrm{forw}}$ 限制为那些我们已知闭式分布的情形。因此,在扩散模型文献中,前向过程里的向量场通常取仿射(affine)形式,即 $ u_t^{\mathrm{forw}}(x)=a_t x $, 其中 $a_t$ 为某个连续函数。
基于上述选择,我们可以使用条件分布(Conditional Distribution)的已知公式 9, 10, 11:
$$ \bar{X}_t \mid \bar{X}_0=z \sim \mathcal{N}\!\big(\alpha_t z,\ \beta_t^2 I_d\big),\quad \alpha_t=\exp\!\Big(\int_0^t a_r\,dr\Big),\quad \beta_t^2=\alpha_t^2 \int_0^t \frac{\big(\sigma_r^{\mathrm{forw}}\big)^2}{\alpha_r^2}\,dr . $$请注意,这些只是高斯(Gaussian)的概率路径(Probability Path)。因此,可以把前向过程(Forward Process)视为构造(高斯)概率路径的一种特例。“概率路径”一词由流匹配(Flow Matching,FM)在 12 中提出,既简化了构造,也使之更通用:其一,扩散模型中的“前向过程”从不真正被模拟(训练时仅从 $\bar p_t(\cdot\mid z)$ 采样);其二,前向过程只在 $t\to\infty$ 时才收敛(也就是说在有限时间内我们永远无法达到 $p_{\text{init}}$)。因此,在本文档中我们选择使用概率路径的表述。
时间反演(Time-Reversal)vs 求解福克–普朗克方程(Fokker–Planck Equation,FPE)#
早期的扩散模型表述并不是通过福克–普朗克方程(或连续性方程(Continuity Equation))来构造训练目标 $u_t^{\text{target}}$ 或 $\nabla \log p_t$,而是通过对前向过程做时间反演13。时间反演 $(X_t)_{0\le t\le T}$ 指一类在时间反转后具有相同轨迹分布的 SDE,即
$$ \mathbb{P}\!\big[\bar{X}_{t_1}\in A_1,\ldots,\bar{X}_{t_n}\in A_n\big]=\mathbb{P}\!\big[X_{T-t_1}\in A_1,\ldots,X_{T-t_n}\in A_n\big],\quad (58) $$$$ \text{对所有 } 0\le t_1,\ldots,t_n\le T,\ \text{且 } A_1,\ldots,A_n\subset S. \quad (59) $$如 Anderson 13 所示,满足上述条件的时间反演可由下式给出:
$$ dX_t=\big[-u_t(X_t)+\sigma_t^2\,\nabla\log p_t(X_t)\big]\,dt+\sigma_t\,dW_t,\quad u_t(x)=u_{T-t}^{\mathrm{forw}}(x),\quad \sigma_t=\sigma_{T-t}. $$由于 $u_t(X_t)=a_t X_t$,上式正对应我们在命题 1 中推导之训练目标的一个特例(这点并非显然,因为各文献的时间约定不同;推导可参见 14)。然而,在生成建模(generative modeling)中,我们通常只使用马尔可夫过程(Markov Process)的终点 $X_1$(例如作为生成图像),并丢弃较早时刻。因此,一个马尔可夫过程究竟是“真正的”时间反演,还是沿着某条概率路径演化,对很多应用并不重要。于是,采用时间反演并非必要且常常次优——例如,概率流常微分方程(Probability Flow ODE)往往表现更好 11 15。所有不同于时间反演的扩散模型采样方案,最终仍需借助福克–普朗克方程。以上也说明了为何当下许多工作直接通过福克–普朗克方程构造训练目标——该路线由 12 16 17 首倡,并在本课程中采用。
流匹配(Flow Matching,FM)与随机插值过程(Stochastic Interpolants,SIs) 12 17#
我们在此介绍的框架与流匹配和随机插值过程最为接近。正如前文所述,流匹配将注意力限定在“流”(flows)本身。事实上,FM 的一个关键创新在于:无需通过前向过程与 SDE 来构造,仅用流模型也能以可扩展的方式完成训练。由于这种限制,要记住:从 FM 模型进行采样时是确定性的(只有初始值 $X_0\sim p_{\text{init}}$ 是随机的)。
随机插值过程既涵盖了“纯流”(pure flow),也包含了我们在此使用的通过朗之万动力学(Langevin dynamics)得到的 SDE 扩展(参见定理 13)。名称“随机插值过程”来自一个插值函数 $I(t,x,z)$,其目的是在两个分布之间进行插值。用我们当前的术语来说,这对应于一种与此前不同但(主要)等价的方式来构造条件与边缘的概率路径(Probability Path)。
与扩散模型(Diffusion Models,DMs)相比,流匹配与随机插值过程的优势在于简单性与通用性兼具:它们的训练框架非常简单,同时又允许你从任意初始分布 $p_{\text{init}}$ 迁移到任意目标分布 $p_{\text{data}}$——而去噪扩散模型通常仅适用于高斯(Gaussian)初始分布与高斯概率路径的情形。这为生成建模(generative modeling)打开了新的可能性,我们将在课程后续简要讨论。
让我们对本节的结果做个小结:
总结 23(Summary 23:训练生成模型,Training the Generative Model)
流匹配(Flow Matching,FM)通过最小化条件流匹配损失(Conditional Flow Matching Loss,CFM Loss)来训练一个神经网络 $u_t^\theta$
条件流匹配损失(conditional flow matching loss):
$$\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{z\sim p_{\text{data}},\ t\sim \mathrm{Unif},\ x\sim p_t(\cdot\mid z)}\!\left[\left\|u_t^\theta(x)-u_t^{\text{target}}(x\mid z)\right\|^2\right] \quad (60)$$其中 $u_t^{\text{target}}(x\mid z)$ 是条件向量场(conditional vector field)(见算法 5)。训练完成后,通过模拟相应的常微分方程(Ordinary Differential Equation,ODE)生成样本(见算法 1)。
若要扩展为扩散模型(Diffusion Model,DM),可使用得分网络(Score Network) $s_t^\theta$,并通过条件得分匹配(Conditional Score Matching,CSM)训练它
条件得分匹配损失/去噪得分匹配损失(conditional score matching loss / denoising score matching loss):
$$\mathcal{L}_{\mathrm{CSM}}(\theta)=\mathbb{E}_{z\sim p_{\text{data}},\ t\sim \mathrm{Unif},\ x\sim p_t(\cdot\mid z)}\!\left[\left\|s_t^\theta(x)-\nabla\log p_t(x\mid z)\right\|^2\right] \quad (61)$$对任意扩散系数 $\sigma_t\ge 0$,模拟如下 随机微分方程(Stochastic Differential Equation,SDE)(如算法 2):
$$X_0\sim p_{\text{init}},\quad dX_t=\Big[u_t^\theta(X_t)+\frac{\sigma_t^2}{2}\,s_t^\theta(X_t)\Big]dt+\sigma_t\,dW_t \quad (62)$$即可生成逼近 $p_{\text{data}}$ 的样本。$\sigma_t\ge 0$ 的最优选择可通过经验方式确定。
高斯概率路径(Gaussian Probability Paths)#
当条件概率路径为高斯
$$p_t(x\mid z)=\mathcal{N}(x;\ \alpha_t z,\ \beta_t^2 I_d),$$则条件得分匹配也称为去噪得分匹配(DSM)。此时,上述两种损失可写为
$$\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},\ z\sim p_{\text{data}},\ \varepsilon\sim\mathcal{N}(0,I_d)}\!\left[\Big\|u_t^\theta(\alpha_t z+\beta_t\varepsilon)-\big(\dot{\alpha}_t z+\dot{\beta}_t\varepsilon\big)\Big\|^2\right],$$$$\mathcal{L}_{\mathrm{CSM}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},\ z\sim p_{\text{data}},\ \varepsilon\sim\mathcal{N}(0,I_d)}\!\left[\Big\|s_t^\theta(\alpha_t z+\beta_t\varepsilon)+\frac{\varepsilon}{\beta_t}\Big\|^2\right].$$在该情形下,无需分别训练 $s_t^\theta$ 与 $u_t^\theta$,因为它们可在训练后互相转换:
$$u_t^\theta(x)=\Big(\beta_t^2\frac{\dot{\alpha}_t}{\alpha_t}-\beta_t\dot{\beta}_t\Big)\,s_t^\theta(x)+\frac{\dot{\alpha}_t}{\alpha_t}\,x .$$同样地,训练完成后,可用算法 2 模拟式(62)的 SDE 来得到样本 $X_1$。
去噪扩散模型(Denoising Diffusion Models,DDMs)#
去噪扩散模型是使用高斯概率路径的扩散模型。因此它们只需学习 $u_t^\theta$ 或 $s_t^\theta$ 中的任一个,二者可相互转换。
虽然流匹配仅支持通过 ODE 的确定性仿真,但上述扩展同时支持确定性仿真(概率流 ODE(Probability Flow ODE,PF-ODE))与随机仿真(SDE 采样)。然而,与能够通过任意概率路径 $p_t$ 将任意初始分布 $p_{\text{init}}$ 迁移到任意目标分布 $p_{\text{data}}$ 的流匹配或随机插值过程不同,去噪扩散模型仅适用于高斯初始分布 $p_{\text{init}}=\mathcal{N}(0,I_d)$ 且概率路径为高斯的情况。
要点(Literature)#
文献中常见的扩散模型等价表述包括:
- 离散时间(Discrete-time):用离散时间马尔可夫链近似 SDE。
- 反向时间记号(Inverted Time Convention):常用 $t=0$ 对应 $p_{\text{data}}$ 的记号(与本文 $t=0$ 对应 $p_{\text{init}}$ 相反)。
- 前向过程(Forward Process):前向/加噪过程是构造(高斯)概率路径的一种方法。
- 通过时间反演构造训练目标(Training Target via Time-Reversal):亦可通过 SDE 的时间反演来构造训练目标——这是本文构造在采用反向时间记号下的一个特例。
5 构建图像生成器(Building an Image Generator)#
在前面的章节中,我们学习了如何训练流匹配(Flow Matching,FM)或扩散模型(Diffusion Model,DM),以便从数据分布 $p_{\text{data}}(x)$ 中采样。这个“配方”是通用的,可适用于多种数据类型与应用。本节我们将学习如何将该框架用于构建图像或视频生成器(例如 Stable Diffusion 3 和 Meta MovieGen Video)。
要构建这样的模型,还缺两味关键材料: 第一,需要形式化条件生成(conditional generation)——本文称为引导(Guidance):例如,如何生成符合特定文本提示的图像,以及如何将现有目标函数恰当地改造以服务这一目的;同时,我们还会介绍无分类器引导(Classifier-Free Guidance,CFG)这一用于提升条件生成质量的常用技术。 第二,讨论常见的神经网络(Neural Network,NN)架构,重点关注图像与视频方向。最后,我们将深入剖析上述两类前沿模型——Stable Diffusion 与 Meta MovieGen——以便了解大规模系统是如何落地的。
5.1 引导(Guidance)#
到目前为止,我们讨论的生成模型都是无条件(unconditional)的,例如图像模型只会生成“某张”图像。然而,任务往往不是生成任意对象,而是在额外信息的条件约束下生成对象。比如,一个图像生成模型可以接收文本提示 $y$,并生成在 $y$ 条件下的图像 $x$。对给定的提示 $y$,我们希望从 $p_{\text{data}}(x\mid y)$(即对 $y$ 条件化的数据分布)中采样。形式化地,令 $y$ 取值于空间 $\mathcal{Y}$。当 $y$ 是文本提示时,$\mathcal{Y}$ 一般是连续空间,如 $\mathbb{R}^{d_y}$;当 $y$ 是离散类别标签时,$\mathcal{Y}$ 为离散集合。在实验室部分我们将使用 MNIST 数据集,此时取 $\mathcal{Y}=\{0,1,\dots,9\}$ 对应手写数字的类别。
为避免“conditional”一词与我们对 $z\sim p_{\text{data}}$(条件概率路径/向量场)的条件化用法在记号与术语上的冲突,本文用 guided 专指对 $y$ 的条件化。
备注 24(Guided 与 Conditional 术语) 在这些讲义中,我们选择用 guided 取代 conditional 来表示对 $y$ 的条件化。我们将据此使用“引导向量场(guided vector field,GVF) $u_t^{\theta}(x\mid y)$”以及“条件向量场(conditional vector field) $u_t^{\text{target}}(x\mid z)$”等表达。该术语体系与文献 14 等保持一致。
因此,引导式生成建模(guided generative modeling)的目标,是能够对任意 $y$ 从 $p_{\text{data}}(x\mid y)$ 中采样。在流匹配(flow matching)与得分匹配(score matching)的语言下(此时生成模型对应于常/随机微分方程(ODE/SDE)的数值模拟),可以如下表述。
关键思想 5(引导式生成模型,Guided Generative Model)
我们将引导式扩散模型定义为:由某个神经网络参数化的引导向量场 $u_t^{\theta}(\cdot\mid y)$,以及一个随时间变化的扩散系数 $\sigma_t$。二者给出为:
- 神经网络: $$ > u^{\theta}:\ \mathbb{R}^d\times\mathcal{Y}\times[0,1]\to\mathbb{R}^d,\quad (x,y,t)\mapsto u_t^{\theta}(x\mid y) > $$
- 固定项: $$ > \sigma_t:\ [0,1]\to[0,\infty),\quad t\mapsto \sigma_t > $$
与“总结 7”相比,区别在于我们额外用输入 $y\in\mathcal{Y}$ 对 $u_t^{\theta}$ 进行了引导。对任意 $y\in\mathbb{R}^{d_y}$,从该模型生成样本的流程为:
- 初始化:$X_0\sim p_{\text{init}}$ (用简单分布(如高斯)初始化);
- 模拟:$dX_t \;=\; u_t^{\theta}(X_t\mid y)\,dt \;+\; \sigma_t\,dW_t$ (将 SDE 从 $t=0$ 模拟到 $t=1$);
- 目标:$X_1\sim p_{\text{data}}(\cdot\mid y)$ (使 $X_1$ 的分布与 $p_{\text{data}}(\cdot\mid y)$ 一致)。
当 $\sigma_t=0$ 时,该模型称为引导式流模型(guided flow model)。
5.1.1 面向流模型的引导(Guidance for Flow Models)#
如果我们设想将 $y$ 固定,并把数据分布取为 $p_{\text{data}}(x\mid y)$,那么就回到了无引导的生成问题;因此可以使用条件流匹配(Conditional Flow Matching,CFM)目标来构建生成模型,即
$$ \mathbb{E}_{z\sim p_{\text{data}}(\cdot\mid y),\;x\sim p_t(\cdot\mid z)} \left\|u_t^{\theta}(x\mid y)-u_t^{\text{target}}(x\mid z)\right\|^2 . \quad (63) $$注意,标签 $y$ 并不会影响条件概率路径(conditional probability path) $p_t(\cdot\mid z)$ 或条件向量场(conditional vector field) $u_t^{\text{target}}(x\mid z)$(尽管原则上可以让其依赖于 $y$)。对所有 $y$ 的选择以及所有 $t\sim\mathrm{Unif}_{[0,1)}$ 展开期望,就得到引导式条件流匹配目标:
$$ \mathcal{L}^{\text{guided}}_{\text{CFM}}(\theta) =\mathbb{E}_{(z,y)\sim p_{\text{data}}(z,y),\,t\sim\mathrm{Unif}_{[0,1)},\,x\sim p_t(\cdot\mid z)} \left\|u_t^{\theta}(x\mid y)-u_t^{\text{target}}(x\mid z)\right\|^2 . \quad (64) $$与式(44)中的无引导目标相比,这里的主要区别之一是我们从 $p_{\text{data}}$ 采样的是联合$(z,y)$,而不是仅采样 $z$。原因在于现在的数据分布在原则上是图像 $z$ 与文本提示 $y$ 的联合分布。实践中,实现式(64)的 PyTorch 数据加载器需要同时返回成批的 $z$ 和 $y$。上述训练过程可导向对 $p_{\text{data}}(\cdot\mid y)$ 的可靠生成。
无分类器引导(Classifier-Free Guidance,CFG)#
尽管理论上,上述条件训练过程是成立的,但很快就有经验发现:按此训练得到的图像样本与期望标签 $y$ 的匹配度仍不足。进一步观察表明,人为增强引导变量 $y$ 的影响可以提升感知质量。该洞见被提炼成广泛用于前沿扩散模型中的技术——无分类器引导(CFG)。为简洁起见,这里仅讨论高斯概率路径(Gaussian probability paths)。回忆式(16),高斯条件概率路径为
$$ p_t(\cdot\mid z)=\mathcal{N}\!\left(\alpha_t z,\;\beta_t^2 I_d\right), $$其中噪声调度器(noise schedulers) $\alpha_t,\beta_t$ 连续可微、单调,并满足 $\alpha_0=\beta_1=0$ 且 $\alpha_1=\beta_0=1$。
为理解 CFG,可利用命题 1(Proposition 1),将引导向量场(guided vector field)用引导得分函数(guided score function) $\nabla\log p_t(x\mid y)$ 重写为
$$ u_t^{\text{target}}(x\mid y)=a_t x + b_t \nabla \log p_t(x\mid y), \quad (65) $$其中
$$ (a_t,b_t)=\left(\frac{\dot{\alpha}_t}{\alpha_t},\; \frac{\dot{\alpha}_t \beta_t^{\,2}-\dot{\beta}_t\,\beta_t \alpha_t}{\alpha_t}\right). \quad (66) $$由贝叶斯法则可将引导得分改写为
$$ \nabla \log p_t(x\mid y) =\nabla \log\!\left(\frac{p_t(x)\,p_t(y\mid x)}{p_t(y)}\right) =\nabla \log p_t(x)+\nabla \log p_t(y\mid x), \quad (67) $$其中梯度 $\nabla$ 对变量 $x$ 求导,因而 $\nabla\log p_t(y)=0$。于是有
$$ u_t^{\text{target}}(x\mid y) =a_t x+b_t\!\left(\nabla \log p_t(x)+\nabla \log p_t(y\mid x)\right) = u_t^{\text{target}}(x)+ b_t \nabla \log p_t(y\mid x). $$上式具有直观结构:引导向量场等于无引导向量场与条件得分之和。由于实证上常见 $x$ 与提示 $y$ 的匹配度不足,一个自然做法是放大 $\nabla \log p_t(y\mid x)$ 的贡献,得到
$$ \tilde{u}_t(x\mid y)=u_t^{\text{target}}(x)+ w\, b_t \nabla \log p_t(y\mid x), $$其中 $w>1$ 被称为引导强度(guidance scale)。需要强调的是,这是一种启发式:当 $w\neq 1$ 时,$\tilde{u}_t(x\mid y)\neq u_t^{\text{target}}(x\mid y)$,即并非真实的引导向量场;然而大量实验表明,当 $w>1$ 时往往能得到更好的生成质量。
备注 25(分类器在哪里?Where is the classifier?) 项 $\log p_t(y\mid x)$ 可以被视为一种针对加噪数据(noised data)的分类器(classifier)——它给出了在给定 $x$ 时标签 $y$ 的似然。事实上,扩散模型(Diffusion Models,DM)的早期工作会训练一个真实的分类器,并按照上文流程将其用于引导,从而得到分类器引导(Classifier Guidance) 18 19。由于该方法已在很大程度上被无分类器引导(Classifier-Free Guidance,CFG)所取代,这里不再详述。
我们再次应用如下等式:
$$ \nabla \log p_t(x\mid y)=\nabla \log p_t(x)+\nabla \log p_t(y\mid x) $$从而得到
$$ \begin{aligned} \tilde{u}\_{t}(x\mid y) &= u_t^{\text{target}}(x) + w\,b_t\,\nabla \log p_t(y\mid x)\\ &= u_t^{\text{target}}(x) + w\,b_t\big(\nabla \log p_t(x\mid y)-\nabla \log p_t(x)\big)\\ &= u_t^{\text{target}}(x) - \big(w a_t x + w b_t \nabla \log p_t(x)\big) + \big(w a_t x + w b_t \nabla \log p_t(x\mid y)\big)\\&= (1-w)\,u_t^{\text{target}}(x) + w\,u_t^{\text{target}}(x\mid y).\end{aligned} $$因此,我们可以把缩放后的引导向量场(scaled guided vector field) $\tilde{u}_t(x\mid y)$ 表达为无引导向量场(unguided vector field) $u_t^{\text{target}}(x)$ 与引导向量场(guided vector field) $u_t^{\text{target}}(x\mid y)$ 的线性组合。一个直接想法是分别训练无引导的 $u_t^{\text{target}}(x)$(例如用式(44))与引导的 $u_t^{\text{target}}(x\mid y)$(例如用式(64)),并在推理时把它们组合得到 $\tilde{u}_t(x\mid y)$。 “等等,我们岂不是要训练两个模型?!” 实际上不必:可以给标签集合增加一个新的记号 $\varnothing$,表示无条件(absence of conditioning)。于是可将 $u_t^{\text{target}}(x)$ 视为 $u_t^{\text{target}}(x\mid\varnothing)$。这样就无需再训练一个独立的模型来强化假想“分类器”的作用。把条件模型与无条件模型合并为同一个模型进行训练(并在推理时放大条件项)的做法,被称为无分类器引导(Classifier-Free Guidance,CFG) 20。
备注 26(一般概率路径的推导 Derivation for general probability paths)
构造
$$\tilde{u}_t(x\mid y)=(1-w)\,u_t^{\text{target}}(x)+w\,u_t^{\text{target}}(x\mid y)$$对任意概率路径(probability path)都成立,而不仅仅是高斯路径。当 $w=1$ 时,显然有 $\tilde{u}_t(x\mid y)=u_t^{\text{target}}(x\mid y)$。我们之所以用高斯路径推导,只是为了阐明该构造背后的直觉,尤其是放大“分类器” $\nabla \log p_t(y\mid x)$ 项的贡献。
训练与“无上下文”引导(Training and Context-Free Guidance)#
现在需要在式(64)的引导式条件流匹配(guided CFM)目标中,加入 $y=\varnothing$(无条件)的可能性。困难在于:当从 $(z,y)\sim p_{\text{data}}$ 采样时,永远不会得到 $y=\varnothing$。因此我们要人为地引入 $y=\varnothing$ 的可能:设超参数 $\eta$ 表示丢弃原始标签 $y$ 并用 $\varnothing$ 取代它的概率。由此得到我们的 CFG 条件流匹配训练目标(CFG conditional flow matching training objective):
$$ \mathcal{L}^{\text{CFG}}_{\text{CFM}}(\theta) =\mathbb{E}_{\square}\big\|u_t^{\theta}(x\mid y)-u_t^{\text{target}}(x\mid z)\big\|^2 \quad (68) $$其中
$$ \square=\ (z,y)\!\sim\! p_{\text{data}}(z,y),\; t\!\sim\!\mathrm{Unif}_{[0,1)},\; x\!\sim\! p_t(\cdot\mid z),\; \text{并以概率 }\eta\text{ 将 }y\text{ 置换为 }\varnothing . \quad (69) $$
图 11:分类器引导的效果。这里的提示词是类别 “Corgi”(一种特定类型的狗)。左:在没有引导的情况下生成的样本(即 (w = 1))。右:在分类器引导且 (w = 4) 时生成的样本。如图所示,无分类器引导(classifier-free guidance)可以提高生成结果与提示词的相似度。图引自文献 [^10]。
总结 27(面向流模型的无分类器引导,Classifier-Free Guidance for Flow Models)
给定无引导的边缘向量场 $u_t^{\text{target}}(x\mid\varnothing)$、引导的边缘向量场 $u_t^{\text{target}}(x\mid y)$,以及引导强度(guidance scale)$w>1$,定义无分类器引导向量场(classifier-free guided vector field)
$$\tilde{u}_t(x\mid y)=(1-w)\,u_t^{\text{target}}(x\mid\varnothing)+w\,u_t^{\text{target}}(x\mid y).\quad (70)$$使用同一个神经网络近似 $u_t^{\text{target}}(x\mid\varnothing)$ 与 $u_t^{\text{target}}(x\mid y)$ 时,可采用如下 无分类器引导的 CFM 目标(CFG-CFM):
$$\mathcal{L}^{\text{CFG}}_{\text{CFM}}(\theta)=\mathbb{E}_{\square}\big\|u_t^{\theta}(x\mid y)-u_t^{\text{target}}(x\mid z)\big\|^2\quad (71) $$其中
$$\square:\ (z,y)\!\sim\! p_{\text{data}}(z,y),\;t\!\sim\!\mathrm{Unif}_{[0,1)},\;x\!\sim\! p_t(\cdot\mid z),\;\text{以概率 }\eta\text{ 将 }y\text{ 置换为 }\varnothing .\quad (72)$$通俗步骤:
- 从数据分布采样 $(z,y)$;
- 在 $[0,1)$ 上均匀采样 $t$;
- 从条件概率路径 $p_t(x\mid z)$ 采样 $x$;
- 以概率 $\eta$ 将 $y$ 置换为 $\varnothing$;
- 令损失为 $\|u_t^{\theta}(x\mid y)-u_t^{\text{target}}(x\mid z)\|^2$,回归到条件向量场。
上述多次用到事实 $u_t^{\text{target}}(x\mid z)=u_t^{\text{target}}(x\mid z,y)$。在推理阶段,给定固定的 $y$,可按下述方式采样:
初始化:$X_0\sim p_{\text{init}}(x)$(用简单分布如高斯)。
模拟:$dX_t=\tilde{u}_t^{\theta}(X_t\mid y)\,dt$ (将 ODE 从 $t=0$ 模拟到 $t=1$)。
样本:输出 $X_1$(目标是让 $X_1$ 服从由 $y$ 引导的语义)。
注意:当 $w>1$ 时,$X_1$ 的分布未必严格等同于 $p_{\text{data}}(\cdot\mid y)$,但经验上其与条件 $y$ 的一致性往往更好;在如 ImageNet($128{\times}128$)与 MNIST 等任务上都能观察到不同引导强度 $w$ 的效果提升。

图 12:在不同引导强度下应用无分类器引导,对手写数字数据集 MNIST 的影响。左:引导强度设置为 $w = 1.0$。中:引导强度设置为 $w = 2.0$。右:引导强度设置为 $w = 4.0$。你将在实验三中自己生成一张类似的图像!
设定: 高斯条件概率路径(Gaussian conditional probability path)
$$ p_t(x\mid z)=\mathcal{N}\!\left(x;\,\alpha_t z,\;\beta_t^{2} I_d\right), $$输入:成对数据集 $(z,y)\sim p_{\text{data}}$,以及神经网络(Neural Network)$u_t^{\theta}$。
对每个 mini-batch 执行:
- 从数据集中采样一对样本 $(z,y)$。
- 采样时间 $t\sim\mathrm{Unif}_{[0,1)}$。
- 采样噪声 $\varepsilon\sim\mathcal{N}(0,I_d)$。
- 设$x=\alpha_t z+\beta_t \varepsilon.$
- 以概率 $p$(即前文的丢弃率 $\eta$)丢弃标签:$y\leftarrow\varnothing$。
- 计算损失
- 对 $\mathcal{L}(\theta)$ 执行梯度下降,更新模型参数 $\theta$。
5.1.2 面向扩散模型的引导(Guidance for Diffusion Models)#
在本节中,我们把上一小节的推理推广到扩散模型。与由式(64)得到目标的方式相同,我们将式(61)的条件得分匹配(Conditional Score Matching,CSM)损失推广为引导式条件得分匹配目标:
$$ \mathcal{L}^{\text{guided}}_{\text{CSM}}(\theta) =\mathbb{E}_{\square}\!\left[\left\|\,s_t^{\theta}(x\mid y)-\nabla\log p_t(x\mid z)\,\right\|^2\right], \quad (73) $$其中
$$ \square=\ (z,y)\!\sim\! p_{\text{data}}(z,y),\; t\!\sim\!\mathrm{Unif},\; x\!\sim\! p_t(\cdot\mid z). \quad (74) $$用式(73)训练得到的引导得分网络(guided score network) $s_t^{\theta}(x\mid y)$,可与引导向量场 $u_t^{\theta}(x\mid y)$ 结合,用于模拟下述 SDE:
$$ X_0\sim p_{\text{init}},\quad dX_t=\Big[u_t^{\theta}(X_t\mid y)+\frac{\sigma_t^2}{2}\,s_t^{\theta}(X_t\mid y)\Big]dt+\sigma_t\,dW_t. $$无分类器引导(Classifier-Free Guidance,CFG)#
现在把无分类器引导扩展到扩散情形。由贝叶斯法则(见式(67)):
$$ \nabla\log p_t(x\mid y)=\nabla\log p_t(x)+\nabla\log p_t(y\mid x), $$因此,对引导强度(guidance scale)$w>1$,可定义
$$ \begin{aligned} \tilde{s}_t(x\mid y) &=\nabla\log p_t(x)+w\,\nabla\log p_t(y\mid x)\\ &=\nabla\log p_t(x)+w\big(\nabla\log p_t(x\mid y)-\nabla\log p_t(x)\big)\\ &=(1-w)\nabla\log p_t(x)+w\,\nabla\log p_t(x\mid y)\\ &=(1-w)\nabla\log p_t(x\mid\varnothing)+w\,\nabla\log p_t(x\mid y). \end{aligned} $$由此得到 CFG 兼容(即考虑 $y=\varnothing$ 的可能)的去噪得分匹配(Denoising Score Matching,DSM)目标:
$$ \mathcal{L}^{\text{CFG}}_{\text{DSM}}(\theta) =\mathbb{E}_{\square}\!\left[\left\|\,s_t^{\theta}(x\mid y)-\nabla\log p_t(x\mid z)\,\right\|^2\right], \quad (75) $$其中
$$ \square=\ (z,y)\!\sim\! p_{\text{data}}(z,y),\; t\!\sim\!\mathrm{Unif}_{[0,1)},\; x\!\sim\! p_t(\cdot\mid z),\; \text{并以概率 }\eta\text{ 将 }y\text{ 替换为 }\varnothing . \quad (76) $$其中 $\eta$ 是一个超参数(将 $y$ 替换为 $\varnothing$ 的概率)。我们把 $\mathcal{L}^{\text{CFG}}_{\text{CSM}}(\theta)$称为引导式条件得分匹配目标(guided conditional score matching objective)。
总结 28(扩散模型的无分类器引导,Classifier-Free Guidance for Diffusions)
给定无引导的边缘得分 $\nabla\log p_t(x\mid\varnothing)$、有引导的边缘得分场 $\nabla\log p_t(x\mid y)$,以及引导强度(guidance scale)$w>1$,定义无分类器引导得分(classifier-free guided score)
$$\tilde{s}_t(x\mid y)=(1-w)\nabla\log p_t(x\mid\varnothing)+w\,\nabla\log p_t(x\mid y).\quad (77)$$利用同一个神经网络(Neural Network)$s_t^{\theta}(x\mid y)$ 同时近似 $\nabla\log p_t(x\mid\varnothing)$ 与 $\nabla\log p_t(x\mid y)$,可使用如下无分类器引导的条件得分匹配(classifier-free guidance CSM,CFG-CSM)目标:
$$\mathcal{L}^{\text{CFG}}_{\text{CSM}}(\theta)=\mathbb{E}_{\square}\left\|\,s_t^{\theta}\big(x\mid (1-\xi)\,y+\xi\,\varnothing\big)-\nabla\log p_t(x\mid z)\right\|^2,\quad (78)$$其中
$$\square=\ (z,y)\!\sim\! p_{\text{data}}(z,y),\;t\!\sim\!\mathrm{Unif}_{[0,1)},\;x\!\sim\! p_t(\cdot\mid z),\;\text{并以概率 }\eta\text{ 将 }y\text{ 替换为 }\varnothing .\quad (79)$$通俗说明(一步式近似):
- $(z,y)\sim p_{\text{data}}(z,y)$ (从数据分布采样);
- $t\sim\mathrm{Unif}_{[0,1)}$ (在区间 $[0,1)$ 上均匀采样);
- $x\sim p_t(x\mid z)$ (从条件概率路径采样 $x$);
- 以概率 $\eta$ 将 $y\leftarrow\varnothing$ (用 $\varnothing$ 取代 $y$);
- $\widehat{\mathcal{L}_{\mathrm{DSM}}^{\mathrm{CFG}}}(\theta) = \|s_t^\theta(x|y) - \nabla \log p_t(x|z)\|^2$(将模型回归到条件得分上)。
在推理阶段,固定 $w>1$,把 $s_t^{\theta}(x\mid y)$ 与引导向量场 $u_t^{\theta}(x\mid y)$ 结合,定义
$$\tilde{s}_t^{\theta}(x\mid y)=(1-w)\,s_t^{\theta}(x\mid\varnothing)+w\,s_t^{\theta}(x\mid y),\\\tilde{u}_t^{\theta}(x\mid y)=(1-w)\,u_t^{\theta}(x\mid\varnothing)+w\,u_t^{\theta}(x\mid y).$$随后按如下方式采样:
- 初始化:$X_0\sim p_{\text{init}}(x)$(用简单分布,如高斯);
- 模拟:$dX_t=\Big[\tilde{u}_t^{\theta}(X_t\mid y)+\frac{\sigma_t^2}{2}\,\tilde{s}_t^{\theta}(X_t\mid y)\Big]dt+\sigma_t\,dW_t,$ 将 SDE 从 $t=0$ 模拟到 $t=1$;
- 样本:输出 $X_1$(目标是让 $X_1$ 符合引导变量 $y$)。
5.2 神经网络架构(Neural Network Architectures)#
下面讨论用于流模型(Flow Models,FMs)与扩散模型(Diffusion Models,DMs)的神经网络设计。具体而言,我们回答:如何构建一个能够表示(引导的)向量场 $u_t^{\theta}(x\mid y)$ 的网络架构? 该网络应有三类输入:向量 $x\in\mathbb{R}^d$、条件变量 $y\in\mathcal{Y}$、时间标量 $t\in[0,1]$;并有一个输出:向量 $u_t^{\theta}(x\mid y)\in\mathbb{R}^d$。
对于低维分布(例如前述玩具数据),用多层感知机(Multi-Layer Perceptron,MLP)参数化 $u_t^{\theta}(x\mid y)$ 即可:把 $x,y,t$ 直接拼接后送入 MLP。 但面对复杂的高维分布(如图像、视频、蛋白质),MLP 往往不够用,通常需要任务特定(application-specific)的专用架构。余下内容我们聚焦于图像(及其扩展的视频)场景,讨论两类常见架构:U-Net 21 与扩散 Transformer(Diffusion Transformer,DiT)。
5.2.1 U-Net 与 扩散 Transformer(Diffusion Transformers,DiT)#
在进入具体架构前,先回忆一个事实:一张图像可被视为向量
$$ x\in\mathbb{R}^{C_{\text{image}}\times H\times W}. $$其中,$C_{\text{image}}$ 表示通道数(channels)(RGB 图像通常有 $C_{\text{input}}=3$,也即 $C_{\text{image}}=3$ 个颜色通道),$H$ 与 $W$ 分别是图像的像素高度(height)与像素宽度(width)。
U-Net#
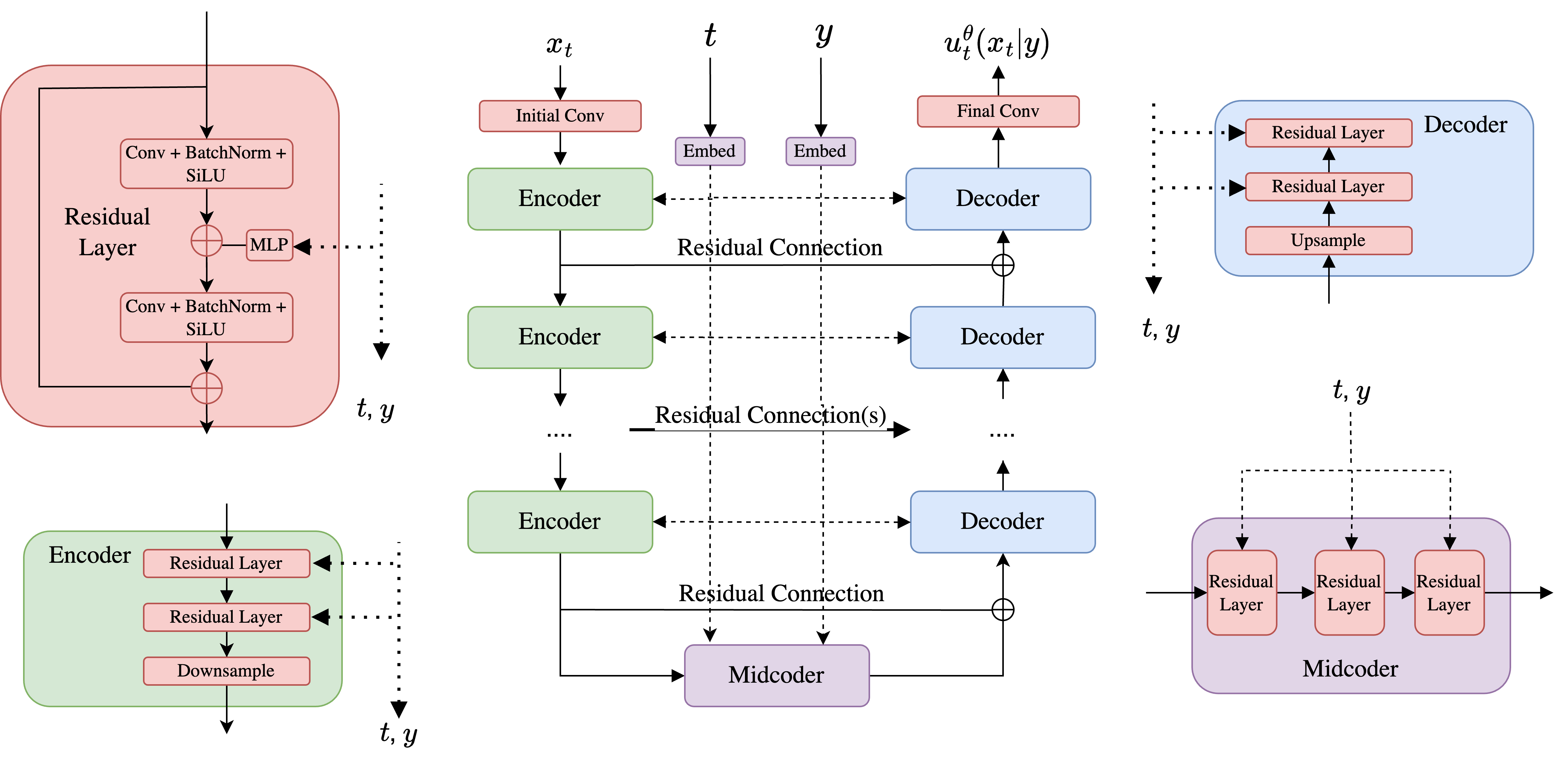
图 13:U-Net 架构的简化示意图。
U-Net 架构 21 是一种特定的卷积神经网络(Convolutional Neural Network,CNN)。它最初为图像分割而设计,其关键特征是:输入与输出都具有图像的形状(通道数可能不同)。这使其非常适合参数化向量场 $x\mapsto u_t^{\theta}(x\mid y)$:在给定 $y$ 时,输入是图像形状,输出同样也是图像形状。因此,U-Net 被广泛用于扩散模型的发展中。
一个 U-Net 由一系列编码器(encoders,记为 $\mathcal{E}_i$)、与之对应的一系列解码器(decoders,记为 $\mathcal{D}_i$)组成,中间夹着一个对潜表征进行处理的块,我们在此称为中编码器(midcoder,记为 $\mathcal{M}$,该术语在文献中并不常用)。以下以尺寸为 $x_t\in\mathbb{R}^{3\times256\times256}$ 的图像为例(即 $(C_{\text{input}},H,W)=(3,256,256)$),展示其在 U-Net 中的处理路径:
$$ x_t^{\text{input}}\in\mathbb{R}^{3\times256\times256} \quad\text{(U-Net 的输入);} $$$$ x_t^{\text{latent}}=\mathcal{E}\!\left(x_t^{\text{input}}\right)\in\mathbb{R}^{512\times32\times32} \quad\text{(经编码器得到潜表征);} $$$$ x_t^{\text{latent}}=\mathcal{M}\!\left(x_t^{\text{latent}}\right)\in\mathbb{R}^{512\times32\times32} \quad\text{(潜表征经中编码器处理);} $$$$ x_t^{\text{output}}=\mathcal{D}\!\left(x_t^{\text{latent}}\right)\in\mathbb{R}^{3\times256\times256} \quad\text{(经解码器恢复输出).} $$注意:当输入穿过编码器时,其表示中的通道数逐步增加,而图像的高度与宽度逐步减小。编码器与解码器通常都由一系列卷积层(夹杂激活函数、池化(pooling)等)构成。未在上式中展开的两点实践细节是:
- 输入 $x_t^{\text{input}}\in\mathbb{R}^{3\times256\times256}$ 常先进入一个预编码块(pre-encoding block)以提升通道数,再送入第一个编码器块;
- 编码器与解码器之间通常通过残差连接(Residual Connections,RCs)相连。
完整结构见图 13。宏观上,大多数 U-Net 都是上述思路的某种变体,但具体设计选择在不同实现中可能差异较大。上文示例选择了纯卷积的实现;而在实际系统中,经常会在编码器与解码器各层中加入注意力层(attention layers)。U-Net 之名来源于其编码器与解码器共同形成的类似字母 “U” 的形状(见图 13)。
扩散 Transformer(Diffusion Transformers,DiTs).#
U-Net 的一种替代方案是扩散 Transformer(DiTs),它们舍弃卷积,只使用注意力(attention) 22 23。DiT 基于视觉 Transformer(Vision Transformers,ViTs),其核心思想是把一张图像切分成若干补丁(patches),为每个补丁做嵌入,然后在补丁之间做注意力计算 24。Stable Diffusion 3(SD3)在使用条件流匹配(conditional flow matching,CFM)训练时,将速度场 $u_t^{\theta}(x)$ 用一种改进版的 DiT 来参数化;第 5.3 节将进一步讨论 25。
备注 29(在潜空间中工作,Working in Latent Space)
大规模应用的一个常见问题是:数据维度过高,内存消耗巨大。例如,若我们希望生成 $1000\times1000$ 分辨率的图像,其维度将达到一百万。为降低内存占用,一个常见设计范式是在潜空间(latent space)中工作,可将其视为数据在更低分辨率下的压缩表示。具体而言,通常的做法是将流模型或扩散模型与一个(变分)自编码器((Variational) Autoencoder,(V)AE)结合:首先用自编码器把训练数据集编码到潜空间,然后在潜空间中训练流/扩散模型。采样过程则先在潜空间中用训练好的流/扩散模型采样,再通过解码器将结果解码回像素空间。直观上,一个训练良好的自编码器能够过滤掉语义上无关的细节,让生成模型“聚焦于”重要且与感知相关的特征 26。到目前为止,几乎所有图像和视频生成的最新方法(state-of-the-art)都在自编码器的潜空间中训练流或扩散模型——即所谓的潜扩散模型(Latent Diffusion Models,LDMs) 26 27。需要注意的是:在训练扩散模型之前,必须先训练好自编码器;而最终性能也强依赖自编码器的质量——即它是否能把图像有效压缩到潜空间,并在解码时恢复出观感优良(aesthetically pleasing)的图像。
5.2.2 引导变量的编码(Encoding the Guiding Variable)#
到目前为止,我们还没有细说引导(条件)变量 $y$ 是如何送入神经网络 $u_t^{\theta}(x\mid y)$ 的。整体上可分两步:先把原始输入 $y_{\text{raw}}$(例如文本提示 “a cat playing a trumpet, photorealistic”)嵌入(embedding)成某个向量形式的输入 $y$,然后再把这个 $y$ 送进实际模型。下面分别说明这两步。
原始输入的嵌入表示(Embedding Raw Input)#
这里考虑两种情形:(1)$y_{\text{raw}}$ 是离散类别标签;(2)$y_{\text{raw}}$ 是文本提示。
若 $y_{\text{raw}}\in\mathcal{Y}\triangleq\{0,\dots,N\}$ 只是类别标签,最简单的做法是:为 $N+1$ 个取值分别学习一个嵌入向量(embedding vector),并把 $y$ 设为该嵌入。嵌入的参数视为 $u_t^{\theta}(x\mid y)$ 的一部分,在训练过程中一并学习。
若 $y_{\text{raw}}$ 是文本提示,情况更复杂,通常依赖冻结的预训练模型(frozen, pre-trained models),把离散文本输入嵌入到能捕获关键信息的连续向量。一个典型选择是 CLIP(Contrastive Language-Image Pretraining,CLIP):CLIP 通过对比学习损失(contrastive loss)在图像与文本提示上学习一个共享嵌入空间,使图像嵌入更接近其对应提示、并远离其他图像/提示 28。于是我们可以令
$$ y=\text{CLIP}(y_{\text{raw}})\in\mathbb{R}^{d_{\text{CLIP}}}, $$即使用冻结的预训练 CLIP 产生的嵌入。在某些场景中,把整个文本压成单个表示可能并不理想;这时可以用预训练 Transformer 对完整提示进行编码,得到一个嵌入序列(sequence of embeddings)。实践中也常把多个此类预训练嵌入组合用于条件输入,以同时获得不同模型的优势 25 29。
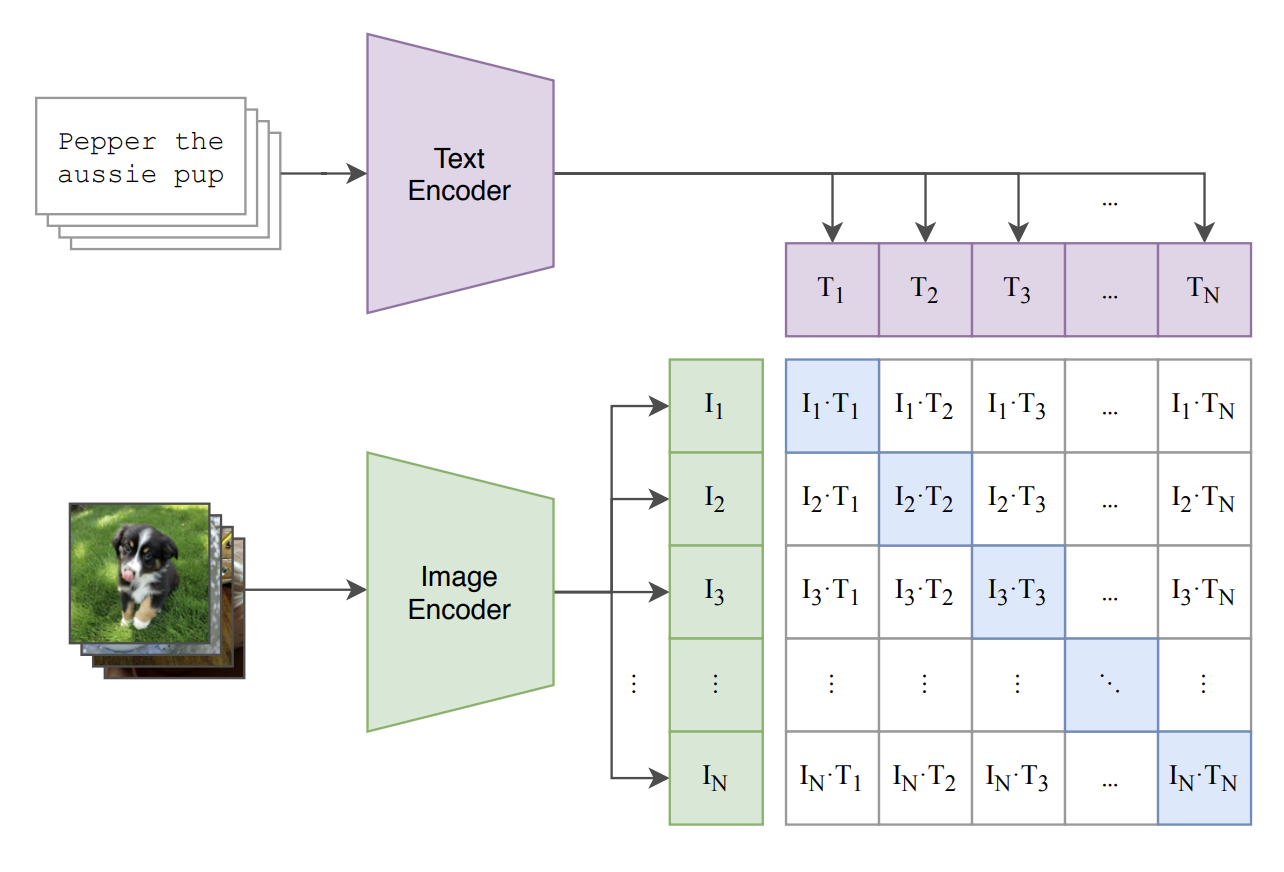
图 14:左:扩散 Transformer 架构的概览,图引自文献 [^19]。右:对比式 CLIP 损失的示意图,其中学习到了一个共享的图文嵌入空间,图引自文献 [^22]。
嵌入表示的输入(Feeding in the Embedding)#
假设我们已经得到嵌入向量 $y\in\mathbb{R}^{d_y}$。接下来怎么做?答案因架构而异,但常见做法是:把 $y$ 以某种方式注入到图像模型的各个子模块。下面简述在实验三所用 U-Net 中的做法(见图 13)。在网络的某个中间位置,我们希望将 $y\in\mathbb{R}^{d_y}$ 的信息注入到当前激活 $x_t^{\text{intermediate}}\in\mathbb{R}^{C\times H\times W}$ 中。可按下面的 PyTorch 风格伪代码进行:
$$ \begin{aligned} &y=\text{MLP}(y)\in\mathbb{R}^{C} &&\text{(将 }y\text{ 从 }\mathbb{R}^{d_y}\text{ 映射到 }\mathbb{R}^{C}\text{)}\\ &y=\text{reshape}(y)\in\mathbb{R}^{C\times1\times1} &&\text{(重塑形状,让它“看起来像图像”)}\\ &x_t^{\text{intermediate}}=\text{broadcast\_add}\!\big(x_t^{\text{intermediate}},\,y\big)\in\mathbb{R}^{C\times H\times W} &&\text{(逐点把 }y\text{ 加到 }x_t^{\text{intermediate}}\text{ 上)} \end{aligned} $$一个常见的例外是:当我们有来自某个预训练语言模型的嵌入序列时,可考虑在(适当切块的)图像与该序列的交叉注意力(Cross-Attention,CA)之间进行条件化。第 5.3 节将给出多种实例。
5.3 大规模图像与视频模型综述(A Survey of Large-Scale Image and Video Models)#
本节最后,我们将简要考察两个大规模生成模型:用于图像生成的 Stable Diffusion 3(SD3),以及 Meta 的用于视频生成的 Movie Gen Video 25 29。如你将看到的,这些模型在我们前文介绍的方法基础上,结合了额外的架构增强以适配更大的规模,并支持结构更丰富的条件模态(例如基于文本的输入)。
5.3.1 Stable Diffusion 3#
Stable Diffusion 是一系列最先进的图像生成模型,也是最早在图像生成中采用大规模潜扩散模型(Latent Diffusion Models,LDMs)的工作之一(可在官方站点体验:https://stability.ai/news/stable-diffusion-3)。
SD3 使用与本文一致的条件流匹配(Conditional Flow Matching,CFM)目标(见算法 5)。注:其论文中对“噪声条件”的记号约定与本文略有不同,但仅是符号差异,算法实质相同。 其论文中系统测试了多种流/扩散的变体,发现流匹配效果最佳。训练时,它采用无分类器引导(Classifier-Free Guidance,CFG)(通过丢弃类别标签的做法),并且像第 5.2 节所述那样,在一个预训练自编码器(Autoencoder,AE)的潜空间(latent space)中进行训练。事实上,训练出一个高质量的自编码器是早期 Stable Diffusion 系列论文的重要贡献之一。
为增强文本条件,SD3 同时使用三种不同类型的文本嵌入:包括 CLIP 嵌入,以及谷歌 T5-XXL 编码器的预训练实例所产生的序列化输出30(做法与 31 32 相似)。其中,CLIP 嵌入提供对输入文本较为粗粒度的整体表征,而 T5 嵌入提供更细粒度的上下文,使模型有能力关注到条件文本中的特定元素。
为适配这些序列化上下文嵌入,作者将扩散 Transformer(Diffusion Transformer,DiT)扩展为不仅对图像的 patch 做注意力,同时也对文本嵌入做注意力;这就把 DiT 原本基于类别的条件机制扩展到基于序列上下文的条件。该改进版 DiT 被称为 多模态 DiT(multi-modal DiT,MM-DiT),如图 15 所示。其最终、最大的模型包含 80 亿参数(8 billion parameters)。在采样时,他们使用 50 步(即网络前向 50 次)、Euler 数值积分方案,并采用 CFG 权重(guidance weight)约 2.0–5.0。
5.3.2 Meta Movie Gen Video#
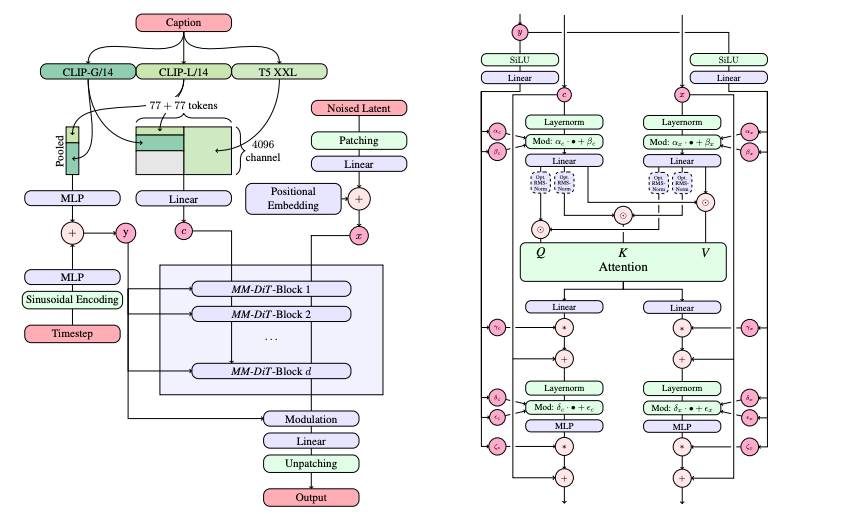
图 15:文献 [^7] 中提出的多模态扩散 Transformer(MM-DiT)架构。该图同样取自文献 [^7]。
接下来介绍 Meta 的视频生成器 Movie Gen Video(项目页:https://ai.meta.com/research/movie-gen/)。由于数据不再是图像而是视频,因此数据 $x$ 位于 $\mathbb{R}^{T\times C\times H\times W}$,其中 $T$ 表示新的时间维(temporal dimension)(即帧数)。正如将看到的,这一视频设置中的许多设计选择,可以看作是把图像领域的既有技术(如自编码器(Autoencoders,AEs)、扩散 Transformer(Diffusion Transformers,DiTs)等)适配到含有额外时间维的场景。
训练与潜空间。 Movie Gen Video 使用与前文相同的条件最优传输路径(CondOT path)下的条件流匹配(Conditional Flow Matching,CFM)目标(见算法 5)。与 SD3 一样,它也在冻结的预训练自编码器的潜空间(latent space)中工作。需要注意的是:为降低内存开销而采用自编码器,在视频任务中比在图像任务中更加重要——这也是目前大多数视频生成器在可生成的视频长度上仍较受限的原因。
具体做法是:作者提出引入一个时间自编码器(Temporal Autoencoder,TAE),将原始视频 $x_t'\in\mathbb{R}^{T'\times 3\times H'\times W'}$ 映射到潜表示 $x_t\in\mathbb{R}^{T\times C\times H\times W}$,其中
$$ \frac{T'}{T}=\frac{H'}{H}=\frac{W'}{W}=8 \quad\text{[21]}. $$为支持长视频,提出了时间拼块(temporal tiling):把视频切分为若干段,分别编码,然后将各段的潜向量拼接(stitched)在一起 29。
主干与注意力。 模型本身(即 $u_t^{\theta}(x_t)$)采用类似 DiT 的主干:沿时间与空间两个维度对 $x_t$ 做补丁化(patchify),随后将这些图像补丁送入 Transformer,内部既有补丁间的自注意力(self-attention),又有与语言模型嵌入(language model embeddings)的交叉注意力(cross-attention),与 SD3 使用的 MM-DiT 思路相似。
文本条件。 Movie Gen Video 使用三类文本嵌入:
其最终、最大的模型拥有 300 亿参数(30 billion parameters)。关于更详尽与系统的说明,建议阅读 Movie Gen 的技术报告 29。
6 致谢(Acknowledgements)#
本课程的顺利开展离不开许多人的慷慨支持。我们特别感谢 Tommi Jaakkola 担任本课程的导师与院系资助人,并在整个过程中提供了深思熟虑的反馈。我们还要感谢 Christian Fiedler、Tim Griesbach、Benedikt Geiger 和 Albrecht Holderrieth 对讲义提出的宝贵意见。
同时感谢 MIT Open Learning 的 Elaine Mello 在课程录制方面的支持,以及 Students for Open and Universal Learning 的 Ashay Athalye 协助剪辑与处理视频。我们还要感谢 Cameron Diao、Tally Portnoi、Andi Qu、Roger Trullo、Ádám Burián、Zewen Yang 以及许多其他同学对实验课(labs)的重要贡献。也感谢 Lisa Bella、Ellen Reid 以及 MIT EECS 的所有同事给予的慷慨帮助。
最后,感谢原始课程(MIT 6.S184/6.S975,于 2025 年 IAP 学期授课)的全体参与者,以及像你这样的读者对本课程的关注。谢谢!
参考文献(References)#
Lawrence Perko. Differential equations and dynamical systems. Vol. 7. Springer Science & Business Media, 2013. ↩︎
Earl A. Coddington, Norman Levinson, and T. Teichmann. Theory of ordinary differential equations. 1956. ↩︎
Arieh Iserles. A first course in the numerical analysis of differential equations. Cambridge University Press, 2009. ↩︎
Xuerong Mao. Stochastic differential equations and applications. Elsevier, 2007. ↩︎
Jascha Sohl-Dickstein et al. “Deep unsupervised learning using nonequilibrium thermodynamics”. In: International conference on machine learning. PMLR. 2015, pp. 2256–2265. ↩︎ ↩︎
Yang Song and Stefano Ermon. “Generative modeling by estimating gradients of the data distribution”. In: Advances in neural information processing systems 32 (2019). ↩︎ ↩︎
Jonathan Ho, Ajay Jain, and Pieter Abbeel. “Denoising diffusion probabilistic models”. In: Advances in neural information processing systems 33 (2020), pp. 6840–6851. ↩︎ ↩︎
Yang Song et al. “Score-based generative modeling through stochastic differential equations”. In: arXiv preprint arXiv:2011.13456 (2020). ↩︎ ↩︎
Simo Särkkä and Arno Solin. Applied stochastic differential equations. Vol. 10. Cambridge University Press, 2019. ↩︎
Yang Song et al. “Score-Based Generative Modeling through Stochastic Differential Equations”. In: International Conference on Learning Representations (ICLR). 2021. ↩︎
Tero Karras et al. “Elucidating the design space of diffusion-based generative models”. In: Advances in Neural Information Processing Systems 35 (2022), pp. 26565–26577. ↩︎ ↩︎
Yaron Lipman et al. “Flow matching for generative modeling”. In: arXiv preprint arXiv:2210.02747 (2022). ↩︎ ↩︎ ↩︎
Brian D. O. Anderson. “Reverse-time diffusion equation models”. In: Stochastic Processes and their Applications 12.3 (1982), pp. 313–326. ↩︎ ↩︎
Yaron Lipman et al. “Flow Matching Guide and Code”. In: arXiv preprint arXiv:2412.06264 (2024). ↩︎ ↩︎
Nanye Ma et al. “Sit: Exploring flow and diffusion-based generative models with scalable interpolant transformers”. In: arXiv preprint arXiv:2401.08740 (2024). ↩︎
Xingchao Liu, Chengyue Gong, and Qiang Liu. “Flow straight and fast: Learning to generate and transfer data with rectified flow”. In: arXiv preprint arXiv:2209.03003 (2022). ↩︎
Michael S. Albergo, Nicholas M. Boffi, and Eric Vanden-Eijnden. “Stochastic interpolants: A unifying framework for flows and diffusions”. In: arXiv preprint arXiv:2303.08797 (2023). ↩︎ ↩︎
Prafulla Dhariwal and Alex Nichol. Diffusion Models Beat GANs on Image Synthesis. 2021. arXiv: 2105.05233 [cs.LG]. url: https://arxiv.org/abs/2105.05233. ↩︎
Yang Song et al. Score-Based Generative Modeling through Stochastic Differential Equations. 2021. arXiv: 2011.13456 [cs.LG]. url: https://arxiv.org/abs/2011.13456. ↩︎
Jonathan Ho and Tim Salimans. Classifier-Free Diffusion Guidance. 2022. arXiv: 2207.12598 [cs.LG]. url: https://arxiv.org/abs/2207.12598. ↩︎
Olaf Ronneberger, Philipp Fischer, and Thomas Brox. “U-net: Convolutional networks for biomedical image segmentation”. In: Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5–9, 2015, proceedings, part III 18. Springer. 2015, pp. 234–241. ↩︎ ↩︎
Ashish Vaswani et al. Attention Is All You Need. 2017. arXiv: 1706.03762 [cs.CL]. url: https://arxiv.org/abs/1706.03762. ↩︎
William Peebles and Saining Xie. Scalable Diffusion Models with Transformers. 2023. arXiv: 2212.09748 [cs.CV]. url: https://arxiv.org/abs/2212.09748. ↩︎
Alexey Dosovitskiy et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. 2021. arXiv: 2010.11929 [cs.CV]. url: https://arxiv.org/abs/2010.11929. ↩︎
Patrick Esser et al. Scaling Rectified Flow Transformers for High-Resolution Image Synthesis. 2024. arXiv: 2403.03206 [cs.CV]. url: https://arxiv.org/abs/2403.03206. ↩︎ ↩︎ ↩︎
Robin Rombach et al. High-Resolution Image Synthesis with Latent Diffusion Models. 2022. arXiv: 2112.10752 [cs.CV]. url: https://arxiv.org/abs/2112.10752. ↩︎ ↩︎
Arash Vahdat, Karsten Kreis, and Jan Kautz. “Score-based generative modeling in latent space”. In: Advances in neural information processing systems 34 (2021), pp. 11287–11302. ↩︎
Alec Radford et al. Learning Transferable Visual Models From Natural Language Supervision. 2021. arXiv: 2103.00020 [cs.CV]. url: https://arxiv.org/abs/2103.00020. ↩︎
Adam Polyak et al. Movie Gen: A Cast of Media Foundation Models. 2024. arXiv: 2410.13720 [cs.CV]. url: https://arxiv.org/abs/2410.13720. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Colin Raffel et al. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. 2019. arXiv: 1910.10683 [cs.LG]. url: https://arxiv.org/abs/1910.10683. ↩︎
Yogesh Balaji et al. eDiff-I: Text-to-Image Diffusion Models with an Ensemble of Expert Denoisers. 2022. arXiv: 2211.01324 [cs.CV]. url: https://arxiv.org/abs/2211.01324. ↩︎
Chitwan Saharia et al. Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding. 2022. arXiv: 2205.11487 [cs.CV]. url: https://arxiv.org/abs/2205.11487. ↩︎
Yi Tay et al. UL2: Unifying Language Learning Paradigms. 2022. arXiv: 2205.05131 [cs.CL]. url: https://arxiv.org/abs/2205.05131. ↩︎
Linting Xue et al. ByT5: Towards a token-free future with pre-trained byte-to-byte models. 2021. arXiv: 2105.13626 [cs.CL]. url: https://arxiv.org/abs/2105.13626. ↩︎
Samuel Lavoie et al. Modeling Caption Diversity in Contrastive Vision-Language Pretraining. 2024. arXiv: 2405.00740 [cs.CV]. url: https://arxiv.org/abs/2405.00740. ↩︎


